Il principio di autorità descrive la propensione ad accettare —o imporre — un’affermazione come vera basandosi sulla reputazione, sul ruolo o sulla notorietà di chi la formula, anziché sulla solidità intrinseca delle prove che la supportano.
Si tratta di una scorciatoia cognitiva che molto spesso può condurre a fallacie logiche, specialmente in ambito scientifico, dove è fondamentale valutare criticamente fonti e argomentazioni.
Un po’ come dire ” …me lo ha detto mio cugino!” e quindi deve essere vero per forza, o “Lo dico io che sono il Megadirettore Galattico Duca Conte etc. e voi altri non avete titoli per smentire le mie affermazioni”
Ma nel mondo reale non funziona così. In contesti scientifici, così come in filosofia e nel diritto, l’autorevolezza deve sempre essere sottoposta a un esame empirico o razionale, al fine di evitare gravi e talvolta grotteschi errori.
Il Cambiamento Climatico non ha niente a che vedere con le variazioni dell’orbita terrestre
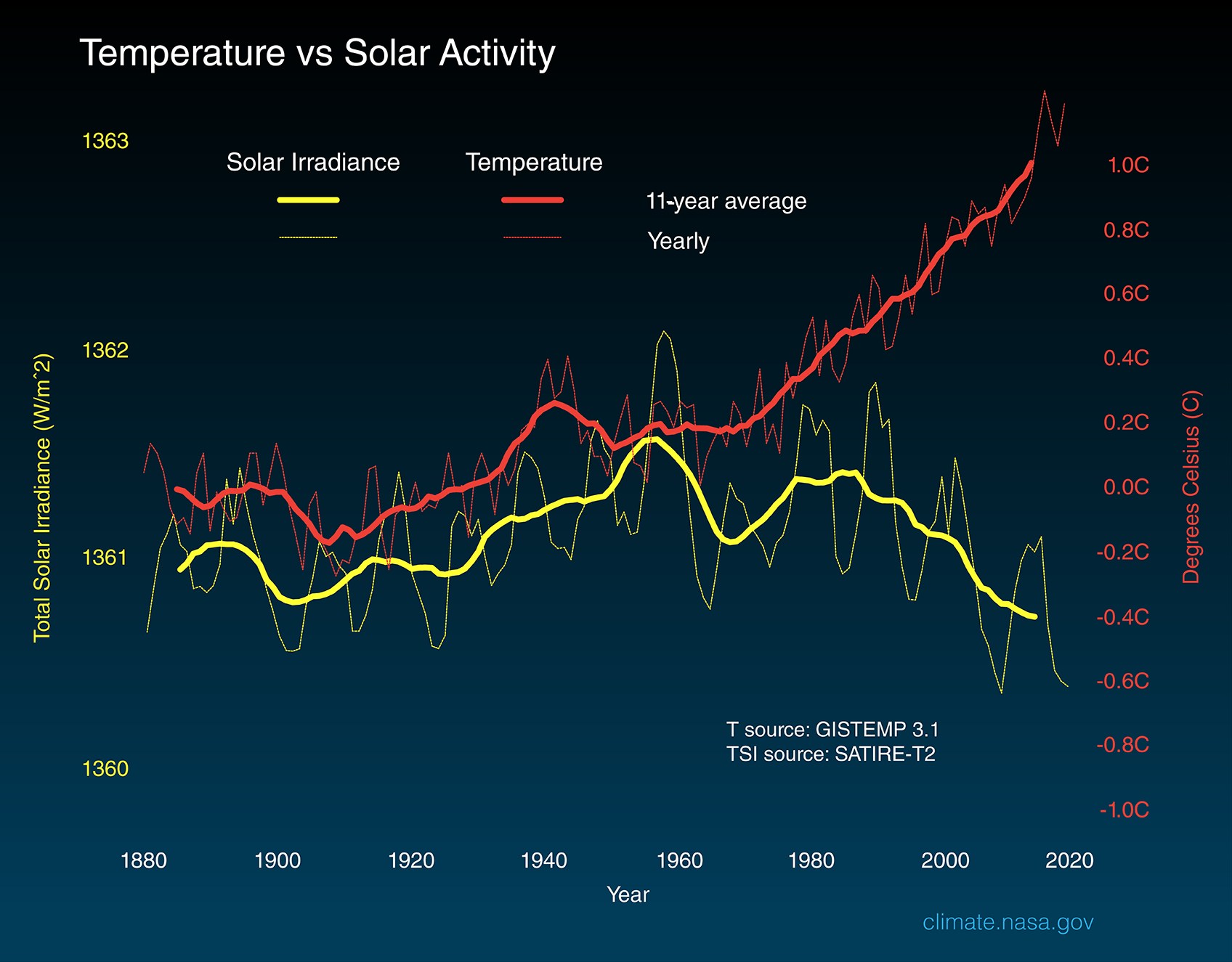
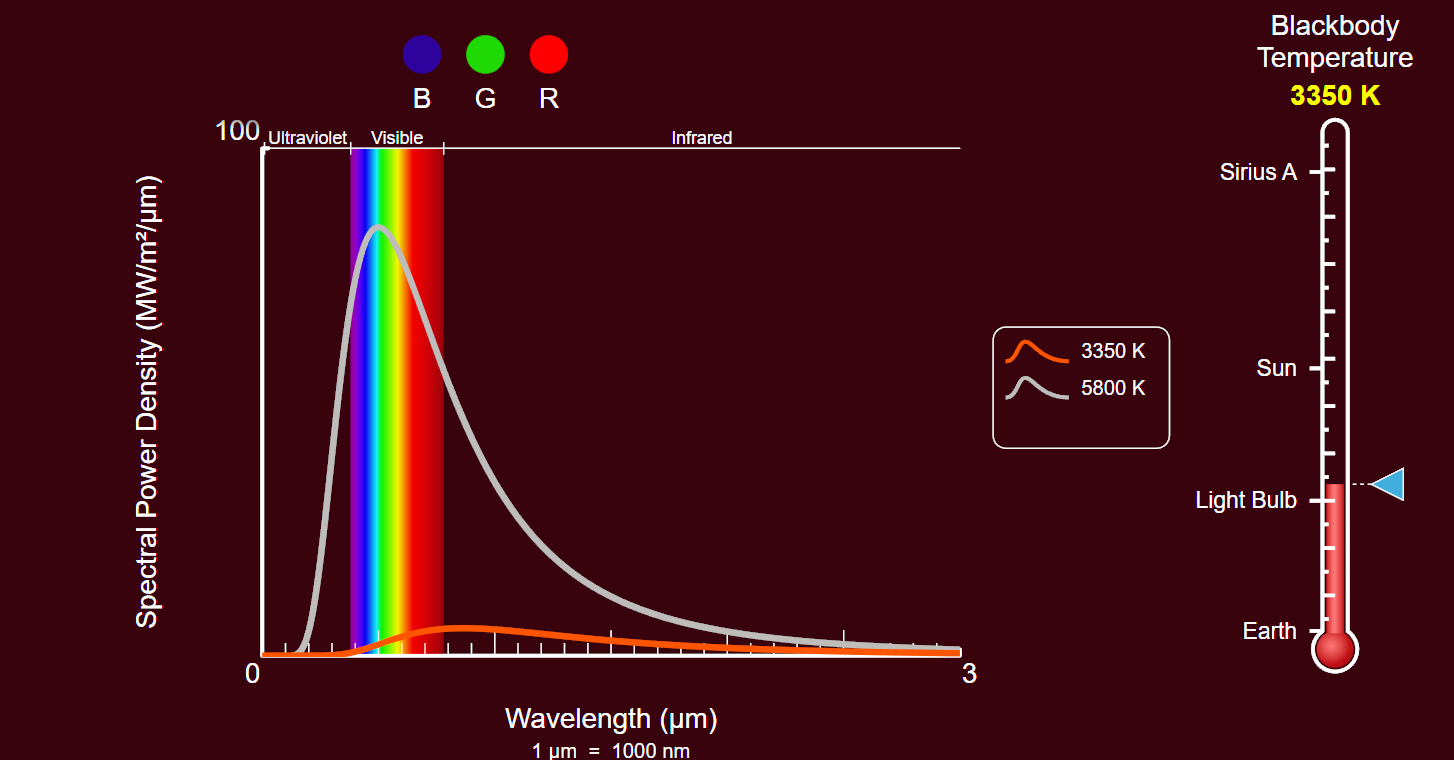
Questo grafico mostra chiaramente due linee che vanno in direzioni opposte: l’irradianza solare totale (TSI, linea gialla): oscillazioni cicliche di ~11 anni (ciclo solare), ma con tendenza a lungo termine in calo (da ~1362 W/m² medi intorno agli anni ’80 a ~1360-1361 negli ultimi decenni) Dati SATIRE-T2 * e temperatura globale (linea rossa, GISTEMP 3.1 **): salita costante e accelerata, da ~0.2°C anomalia negli anni ’80 a +1.0°C+ oggi (rispetto al riferimento base 1951-1980, la tendenza è inequivocabile).
Nel mio recente articolo La CO₂ non è cibo per le piante: chimica reale contro bufale climatiche [1] ho smontato unna congettura fatalista tanto cara a coloro che, dopo aver negato per anni ogni evidenza che dimostrava l’aumento antropogenico della \(CO_{2}\), cercavano di farla digerire affermando che la \(CO_{2}\) è cibo per le piante.
Un’altra congettura cara ai climapiattisti più puri e negazionisti è quella di attribuire il Riscaldamento Climatico Antropogenico a non meglio precisate variazioni dell’orbita terrestre (ora colpa di Giove, ora di Venere, ora di entrambi) come nella miglior tradizione ‘strologica 1 fino a scomodare i Cicli di Milankovitch (fa sempre ganzo usare termini e fenomeni che realmente non si comprendono giusto per darsi una certa importanza).
Non avendo altre argomentazioni a supporto delle loro congetture, nelle loro comparsate nelle trasmissioni-pollaio 2 in televisione questi vecchi arnesi iniziano la loro solita sequela di anatemi snocciolando titoli accademici e incarichi ricoperti con la presunzione di essere gli unici a poter parlare di Riscaldamento Globale verso chiunque gli si opponga, siano essi scienziati o attivisti informati.
L’orbita terrestre
Partiamo dai dati veri: Senza risalire oltre, diciamo dall’eone Proterozoico (2,5 miliardi di anni fa), l’orbita terrestre sempre rimasta stabile a una distanza media di 149,6 milioni di chilometri [2].
Questo accade perché la massa della Terra (o meglio, del sistema Terra-Luna) è relativamente grande rispetto agli altri corpi minori e non subisce perturbazioni estreme da parte dei giganti gassosi del Sistema Solare, checché ne dicano gli ‘strologi.
Insomma, vista dalla Terra, la struttura complessiva del Sistema Solare è dinamicamente tranquilla e — per nostra fortuna — piuttosto noiosa.
Gli unici eventi che potrebbero alterare drasticamente l’orbita terrestre sono:
- incontri ravvicinati con pianeti massicci,
- passaggi di stelle vicine,
- instabilità dinamiche del Sistema Solare.
Le ricostruzioni geologiche e astronomiche, però, non mostrano tracce di sconvolgimenti orbitali nel periodo fin qui considerato.
Geometria astronomica for dummies
1) Energia orbitale e semiasse maggiore
Per un’orbita kepleriana attorno a una stella, il semiasse maggiore \(a\) è legato all’energia specifica orbitale \(\epsilon\):
\[ \epsilon = – \tfrac{\mu}{2a} \]
dove
- \(\mu = GM_{\odot}\) è il parametro gravitazionale 3
- \(a\) è il semiasse maggiore
- \(\epsilon\) è l’energia per unità di massa
Se non sono presenti altre forze dissipative, ma solo gravità newtoniana, \(\epsilon\; \text{e}\; a\) sono costanti. Le altre perturbazioni planetarie alterano l’eccentricità, l’inclinazione, gli argomenti angolari, ma il semiasse maggiore resta praticamente invariato al primo ordine.
2) Perché le variazioni sono minime: le equazioni di Lagrange per \(a\)
In teoria, il semiasse maggiore può variare per effetto di un potenziale perturbativo \(R\)
(dovuto agli altri pianeti, ecc.). Le equazioni planetarie di Lagrange danno:
\[ \tfrac{da}{dt}=\tfrac{2}{na} \tfrac{\partial R}{\partial M} \]
dove
- \(n =\sqrt{\tfrac{\mu}{a^3}}\) è il moto medio
- \(M\) è l’anomalia media
- \(R\) è il potenziale perturbativo medio
Facendo la media su molte orbite (per esempio con approssimazione secolare, il termine \(\tfrac{\partial R}{\partial M}\) tende a zero:
\[ \left\langle \tfrac{da}{dt} \right\rangle \approx 0 \]]
ovvero il semiasse maggiore può oscillare, ma non deriva mai sistematicamente [3].
3) Effetto della perdita di massa solare
E qui la cosa si fa parecchio interessante. Tutte le stelle durante tutto il loro ciclo vitale perdono una piccola frazione della propria massa sotto forma di vento stellare e radiazione; anche il Sole non fa eccezione
Se la massa del Sole diminuisce nel tempo (\(M_{\odot} \)) diminuisce lentamente nel tempo, il parametro gravitazionale \(\mu =\;GM_{\odot}\) si riduce e le orbite dei pianeti si espandono.
Per un lento calo della massa centrale, al primo ordine vale la relazione (problema kepleriano a due corpi):
\[\tfrac{\overset{.}a}{a} \approx – \tfrac{\overset{.}M_{\odot}}{M{\odot}}\]
dove \(a\) è il semiasse maggiore dell’orbita terrestre.
Assumendo \(\tfrac{\overset{.}M_{\odot}}{M{\odot}}\) circa costante su tempi geologici, si integra ottenendo:
\[ a(t) \approx a_{0} \tfrac{M_{\odot} \;(0)}{M_{\odot} \;(t)} \]
Osservazioni e modelli suggeriscono per il Sole un tasso relativo di perdita di massa dell’ordine di:
\[ \tfrac{\overset{.}M_{\odot}}{M{\odot}} \approx 9 \times 10^{-14}\;yr^{-1} \]
somma di vento solare e conversione massa–energia. Prendiamo così il nostro intervallo di tempo dal Proterozoico:
\[t=2.5 \times 10^{9}\;\text {anni} \]
Con \(a_{0} \simeq 1,496\times 10^{8}\;km \), la variazione al primo ordine del semiasse maggiore è:
\[ \Delta a \simeq a_{0}\left| \tfrac{\overset{.}M_{\odot}}{M{\odot}} \right|t\]
sostituendo i valori:
\[ \Delta a \simeq 1,496 \times 10^{8}\;km \times 8,95 \times 10^{-14}\;yr^{-1}\times 2,5 \times 10^{9}\;yr \]
Pertanto:
\[ \Delta a \approx1,496 \times 10^{8}\;km \times 2,2375 \times 10^{-4} \approx 3,35 \times 10^{4}\;km \]
In altri termini, dal Proterozoico (2.5 miliardi di anni fa) il semiasse maggiore dell’orbita terrestre è aumentato di 33500 chilometri su una distanza di 149,6 milioni di chilometri.
\[ \tfrac{\Delta a}{t} \approx \tfrac{3,35\times 10^{4}\;\text{km}}{2,5\times^{9}\;\text{anni}}\sim 1,34 \;\text{cm/anno} \]
Un’inezia, se oggi, con un’eccentricità dell’orbita di 0,0167 (quasi circolare) la differenza tra afelio e perielio è di \(4.999.627\; km \approx 5 \times 10^{6}\;km\).
Ma mica è finita qui.
4) La formula di Gough [4]
Il Sole, proprio come tutte le altre stelle di tipo G nel Ramo Principale, aumenta lentamente la propria luminosità mentre:
- converte idrogeno in elio nel nucleo
- il nucleo si contrae
- la temperatura centrale aumenta
- la potenza irradiata cresce
I modelli di evoluzione solare mostrano una crescita quasi lineare su scale di centinaia di milioni di anni.
\[ \tfrac{L(t)}{L_{0}} \approx 1-\tfrac{2}{5}\left( 1-\tfrac{t}{t_{0}} \right) \]
ovvero un aumento di luminosità di circa il 30% da quando è nato il Sole. Un tasso medio ≈ 0,7% ogni 100 milioni di anni. Ai fini pratici, un aumento di luminosità di questa portata comporta un aumento della costante solare di \(9-10\;W/m^{2}\), ossia \(\sim 1^{\circ}C \) ogni 100 milioni di anni. Anche qui, neanche il 2% rispetto al Proterozoico.
Concludendo questa prima carrellata tra geometria astronomica e astrofisica cari pseudoesperti climapiattisti non sono le orbite o la luminosità solare i responsabili del Riscaldamento Globale.
Ma so di certo che tirereste la scusa: Ma allora i Cicli di Milankovitch?
I Cicli di Milankovitch
I cicli di Milankovitch descrivono i cambiamenti a lungo termine nella traiettoria terrestre, proposta negli anni ’20 dal geofisico e astronomo Milutin Milankovitch. Egli analizzò le variazioni dell’eccentricità terrestre, dell’inclinazione dell’asse e della precessione orbitale avvenute negli ultimi milioni di anni, individuando la correlazione tra tali parametri e i modelli climatici del pianeta, in particolare i cicli glaciali.
Attualmente, la precessione assiale della Terra completa un intero ciclo di precessione all’incirca in ~ 26.000 anni.
Ma in un lontano passato non era così. La canonica interpretazione dei ciclo di Milankovitch non va oltre i 50 milioni di anni.
1) La precessione assiale

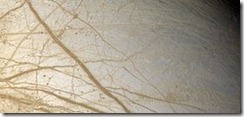
Regolari alternanze di strati bianchi, marrone-rossastri e grigio-blu, su una scala di circa 10 cm, sono interpretate dai ricercatori come tracce del ciclo di precessione dell’asse terrestre, visibile in primo piano a sinistra nell’immagine. Circa 2,46 miliardi di anni fa, tale ciclo aveva un periodo sensibilmente più breve – intorno agli 11.000 anni – rispetto agli attuali circa 21.000 anni, a causa della minore distanza tra Terra e Luna. La determinazione precisa del periodo dei cicli su piccola scala, e quindi della distanza Terra-Luna, può essere ottenuta confrontando il rapporto di spessore con i cicli su scala maggiore di 100.000 anni, osservabili sullo sfondo.
Credit: Frits Hilgen
Anche questa volta la geologia e la matematica ci sono di aiuto per ricostruire la storia — e la climatica — della Terra. Oggi la durata del giorno è di ~24 ore e la frequenza precessionale (precessione lunisolare o assiale) è ≈ 50,3″ per anno.
\[ \tfrac{360\;^{\circ}}{ 50,3^{\prime\prime}/anno} = \;\approx 25786 \; anni\]
Ma nel Proterozoico [5] non era così. il giorno durava 17 ore e la Luna era ad appena ≈ 216-220 mila chilometri di distanza. E siccome la frequenza di precessione \(\psi\) è direttamente proporzionale al reciproco della velocità angolare di rotazione terrestre \(\omega\):
\[ \psi \propto \tfrac{1}{\omega} \]
Non è quindi difficile dimostrare che nel Proterozoico il ciclo precessionale era molto più breve di oggi del 41%.
2) La precessione del perielio
Parallelamente, la rotazione ellittica dell’orbita influisce sull’alternanza delle stagioni e sulle variazioni orbitali con un periodo lento di ~ 112 mila anni. Questa si chiama precessione del perielio (o della linea degli apsidi).
Anch’essa non è costante nel tempo. È cambiata in modo significativo, ma per ragioni completamente diverse rispetto alla precessione degli equinozi.
La precessione del perielio è un movimento della stessa orbita ellittica terrestre. È causata principalmente dalle attrazioni gravitazionali degli altri pianeti, specialmente Giove e Saturno. La sua durata dipende quindi dalla configurazione del Sistema Solare.
Secondo il modello più accreditato, noto come Modello di Nizza e le sue successive evoluzioni [6], i pianeti giganti del Sistema Solare (Giove, Saturno, Urano e Nettuno) non si sono originati nelle attuali posizioni orbitali. Le interazioni gravitazionali con il disco residuo di gas e planetesimi, avvenute nel corso di lunghi periodi, hanno determinato la migrazione delle loro orbite. Questo processo graduale ha modificato in modo costante le influenze gravitazionali esercitate da ciascun pianeta sull’orbita terrestre, causando variazioni nel periodo della precessione del perielio.
Il Sistema Solare si configura come un sistema dinamico intrinsecamente caotico su scale temporali dell’ordine di milioni di anni. In tale contesto, le orbite planetarie non possono essere previste con precisione indefinita: piccole perturbazioni tendono ad amplificarsi, generando variazioni non lineari nei parametri orbitali, compreso il ciclo della precessione del perielio.
Nel recente passato geologico, ossia negli ultimi pochi milioni di anni, la durata di questo ciclo ha variato tra circa 100.000 e 130.000 anni, attestandosi intorno ai ~ 112.000 anni durante il Quaternario, con un impatto significativo sull’insorgenza delle ere glaciali.
Risalendo a centinaia di milioni di anni fa, nel Proterozoico, la configurazione orbitale della Terra era quasi certamente differente, determinando una durata diversa del ciclo. La stima esatta di tale valore è estremamente complessa, ma i modelli dinamici confermano che non si trattava di un parametro costante.
È fondamentale distinguere che questo ciclo è del tutto indipendente dalla presenza o dalla distanza della Luna. Quest’ultima influisce fortemente sulla precessione degli equinozi e sulle maree, ma esercita un’influenza trascurabile sull’orbita ellittica terrestre attorno al Sole, governata principalmente dall’interazione con gli altri pianeti.
3) La precessione climatica
Quest’altro ciclo di Milankovitch è invece la combinazione dei due illustrati qui sopra. È quindi abbastanza evidente che anche questo, attualmente lungo ~ 21 mila anni, è in realtà piuttosto variabile:
\[ \tfrac{1}{P_{clim}}= \tfrac{1}{P_{assiale}} + \tfrac{1}{P_{orbitale}} \]
In altre parole L’asse terrestre ruota (ciclo lento) e contemporaneamente l’intera ellisse orbitale ruota (ciclo ancora più lento). La posizione relativa tra la direzione dell’asse (che definisce le stagioni) e la direzione del perielio (il punto dell’orbita più vicino al Sole) cambia con una velocità che è la somma delle due velocità di rotazione. Ecco perché il periodo risultante è più corto di entrambi.
4) L’eccentricità dell’orbita
I cicli di Milanković NON sono “fissi”: derivano da frequenze secolari dei pianeti, chiamate:
g₁, g₂, g₃, g₄, g₅… (precessione dei perieli)
s₁, s₂, s₃, s₄, s₅… (precessione dei nodi)
Le frequenze gₙ (precessione dei perieli)
| Pianeta | Simbolo | gₙ (arcsec/anno) | Ruolo |
|---|---|---|---|
| Mercurio | g₁ | +5.59 | irrilevante per la Terra |
| Venere | g₂ | +7.45 | fondamentale per il ciclo di 405 mila anni |
| Terra | g₃ | +17.35 | precessione orbitale terrestre |
| Marte | g₄ | +17.92 | modula i cicli da 100 mila e 2.4 milioni di anni |
| Giove | g₅ | +4.25 | modula il ciclo di 405 mila anni |
Le frequenze sₙ (precessione dei nodi)
| Pianeta | Simbolo | sₙ (arcsec/anno) | Ruolo |
|---|---|---|---|
| Mercurio | s₁ | –5.59 | marginale |
| Venere | s₂ | –7.06 | influenza obliquità |
| Terra | s₃ | –18.85 | ciclo obliquità di 41 mila anni |
| Marte | s₄ | –17.75 | modula obliquità e cicli lunghi |
| Giove | s₅ | –6.57 | contributo minore |
Questa spesso è una parte che pochi si soffermano a spiegare.
- Il Ciclo “Ancorato” di 405.000 anni
Questo ciclo ultra-lungo è principalmente una risonanza orbitale tra la precessione del perielio di Venere e quella della Terra. In parole povere, i punti dell’orbita più vicini al Sole (perielio) di questi due pianeti si “inseguono” nello spazio con un ritmo fisso e stabile, completando un ciclo completo ogni 405.000 anni.
Giove, con la sua enorme massa, è il grande regolatore che rende possibile questa risonanza. La sua gravità domina la precessione del perielio di tutti i pianeti interni (Mercurio, Venere, Terra, Marte).
\[ P= \tfrac{1}{\mid g_{_{2}}\;-\;g_{_{5}}\;\mid} \]
Senza l’influenza stabilizzante di Giove, le orbite dei pianeti interni mostrerebbero un comportamento molto più caotico. Quindi, è più preciso dire: il ciclo di 405.000 anni è una risonanza tra Venere e Terra mediata dalla gravità di Giove.
Stabilità: Questo è il ciclo di Milankovitch più stabile nel tempo. I calcoli e le evidenze geologiche suggeriscono che sia rimasto costante per almeno 250 milioni di anni e probabilmente per gran parte dell’era Fanerozoica. Per questo è chiamato il “pendolo geologico” o “cronometro” per calibrare la scala dei tempi geologici profondi. - I Cicli di ~100.000 e ~400.000 anni (Eccentricità)
Questi cicli derivano dalla modulazione dell’eccentricità dell’orbita terrestre. Non sono semplici risonanze a due corpi, ma emergono dalla combinazione di cicli più brevi legati alle interazioni tra più pianeti.
L’eccentricità \(e\) della Terra varia perché la sua orbita è continuamente perturbata dalle attrazioni degli altri pianeti. Matematicamente, la variazione di \(e\) può essere scomposta in una somma di molte componenti sinusoidali con periodi diversi.
Un ciclo di ~100.000 anni: Questo è il risultato della combinazione di altri due cicli principali: uno
legato alle interazioni Terra-Giove-Saturno, con un periodo di circa 95.000 anni e l’altro legato alle interazioni Terra-Marte, con un periodo di circa 99.000 anni (a volte citato come 120.000 anni, a seconda del modello) [7].
La sovrapposizione (interferenza) di questi due segnali produce il picco di potenza dominante che osserviamo nei dati climatici degli ultimi milioni di anni intorno ai 100.000 anni.
Ciclo di ~400.000 anni: Questo è un armonico del ciclo di 405.000 anni (\(\sim 405/1 = 405 \;\text{e}\; 405/4 ≈ 101\)), ma anche il risultato di altre interazioni a lungo termine nel sistema solare.
Questo contesto illustra il motivo per cui il ciclo glaciale di circa 100.000 anni, caratteristico degli ultimi 800.000 anni, rimane uno dei fenomeni più enigmatici e dibattuti della paleoclimatologia. Il forcing astronomico legato all’eccentricità, su questa scala temporale, risulta infatti estremamente debole, producendo solo lievi variazioni di insolazione. Perché questo segnale minimo diventi il ciclo glaciale predominante, il sistema climatico terrestre – comprendente calotte di ghiaccio, oceani e concentrazioni atmosferiche di \(CO_{2}\) – deve rispondere in modo non lineare e con meccanismi di amplificazione significativi.
In epoche geologiche più remote, quando la disposizione dei continenti o i livelli di \(CO_{2}\) differivano sensibilmente, altri cicli astronomici, come quello di 41.000 anni legato alle variazioni dell’obliquità, esercitavano un’influenza dominante sulle oscillazioni climatiche globali.
Cicli di Milankovitch
| Fenomeno | Periodo | Causa | Pianeti coinvolti |
|---|---|---|---|
| Eccentricità lunga | 405 mila anni | Risonanza g₂ - g₅ | Venere + Giove |
| Eccentricità breve | 95-125 mila anni | g₄ dominante | Marte |
| Eccentricità molto lunga | 2,4 milioni anni | g₃ - g₄ | Terra + Marte |
| Obliquità | 41 mila anni | s₃, s₄ | Terra + Marte |
| Precessione assiale | 25786 anni | coppia Sole + Luna | — |
| Precessione orbitale | 112 mila anni | g₃ | Terra |
| Precessione climatica | 19-23 mila anni | combinazione | Terra + Marte + Giove |
sₙ = frequenze di precessione dei nodi (piani orbitali)
Tutti i periodi, eccetto il primo che è stabile, si riferiscono ai periodi attuali.
Conclusione
I Cicli di Milankovitch non sono di certo una novità per chi segue da vicino l’astronomia. E le risonanze gravitazionali dei pianeti vicini (Venere e Marte) e dell’imponente nostro gigante gassoso (Giove, ma in misura minore anche Saturno) che agiscono sulla linea delle absidi e l’eccentricità dell’orbita planetaria non sono una scoperta dei climapiattisti di oggi.
Ho anche dimostrato, casomai ce ne fosse bisogno per qualche incauto senza mestiere, che il semiasse maggiore dell’orbita terrestre è costante nel tempo (non lo dico io ma le leggi di Keplero).
Quindi no. non ci sono state negli ultimi 170 anni variazioni orbitali repentine o fluttuazioni nella luminosità/temperatura del Sole [8] per giustificare il riscaldamento globale in atto [9].
Vedere poi, che tra i peggiori negazionisti italiani figurano anche alcuni professori universitari, mi provoca sgomento.
Come si può leggere, da uno stralcio del loro manifesto del 17 giugno 2019, riportato qui a fianco, di strafalcioni ne vedo parecchi, a cominciare dal loro motto che la \(CO_{2}\) non è un inquinante ma che è indispensabile alla vita del pianeta.
Ma sicuro, senza una atmosfera la temperatura di equilibrio della Terra sarebbe intoro ai 255 °K, ossia -18 °C. Ma la presenza di una atmosfera con una modesta quantità di anidride carbonica compresa tra i 200 e 300 ppm permette di avere una temperatura media planetaria compresa fra i 13 e i 15 °C, poco sopra il punto triplo dell’acqua.
I climapiattisti nostalgici di oggi spesso riportano le condizioni climatiche del Giurassico come esempio di come la vita prosperava sulla Terra nonostante che l’anidride carbonica atmosferica fosse ben più abbondate di oggi
In quell’era si verificarono tuttavia episodi di riscaldamento globale che determinarono crisi ecologiche e marine: picchi termici provocarono ampie zone oceaniche povere di ossigeno e estinzioni di massa, evidenziando la vulnerabilità degli ecosistemi ai cambiamenti climatici.
Nel Mesozoico, incluso il Giurassico, la Terra si trovava in una fase di “clima serra”, molto più caldo rispetto a oggi: l’innalzamento del livello marino favorì la formazione di rocce sedimentarie marine, tipiche di ambienti caldi e umidi. Nei periodi di intenso riscaldamento (eventi anossici oceanici), legati a concentrazioni di \(CO_{2}\) fino a 1000-1500 ppm, causarono fioriture algali e gravi estinzioni marine.
Tornando al presente, invece la specie umana e la sua civiltà si sono tuttavia evoluti in condizioni molto diverse da quelle del Giurassico, con temperature medie globali di 14-15 °C e \(CO_{2}\) intorno a 250-280 ppm; nel Giurassico, L’Umanità non si sarebbe mai potuta evolvere fino allo stadio odierno.
Ridentem dicere verum: quid vetat?
È un’antica locuzione latina del poeta romano Orazio, che oggi potremmo riassumere in Arlecchino si confessò burlando.
In questo caso, potremmo riassumere tutto il pomposo manifesto negazionista climatico nella sua più semplice e provocatoria frase: data la fondamentale importanza dei combustibili fossili per l’approvvigionamento energetico globale, si raccomanda di evitare politiche di riduzione indiscriminata delle emissioni di anidride carbonica.
Questo è il vero messaggio che si cela dietro al negazionismo climatico e ai deliranti sproloqui sui social dei climapiattisti: le variazioni orbitali della Terra, i cicli di Milankovitch, la \(CO_{2}\) è cibo per le piante [10], e tutte le altre menate possibili e immaginabili — fino a inventarsi falsi storici — per sostenere che l’eccesso di anidride carbonica rispetto ai livelli preindustriali non è responsabile del Riscaldamento Globale non è scientificamente sostenibile.