[latexpage]
Riuscire ad immaginare oggi un buco nero non è difficile, anzi. La fantascienza del XX secolo e il cinema hanno reso i buchi neri talmente familiari quasi da distorcerne il significato. Per la fisica invece sono semplicemente delle regioni di spazio dove materia – o energia – è collassata oltre una certa densità critica, dove la velocità di fuga supera anche la velocità della luce. Tutto quello che è o finisce all’interno di questa regione di spazio si suppone converga verso una singolarità, ovvero un punto geometrico di densità infinita, questo almeno per la meccanica relativistica. Il confine tra questa regione di spazio collassato e il resto dell’universo si chiama orizzonte degli eventi, sede di tutta una serie di bizzarri fenomeni quantistici ancora lungi dall’essere pienamente compresi.
La storia dei buchi neri

Credit: P. Marenfeld / NOAO / AURA / NSF, via Gemini Observatory at http://www.gemini.edu/node/11703
Il concetto di buco nero nacque molto prima della Relatività Generale. Verso la fine dell’Settecento, quando la Meccanica di Newton sembrava fosse in grado di spiegare la gravità, all’astronomo inglese John Michell (che per primo fornì un’accurata misura della costante gravitazionale) e, successivamente, il marchese Pierre-Simon Laplace, uno dei più grandi scienziati del periodo napoleonico, ebbero indipendentemente l’idea che potessero esistere corpi celesti con una velocità di fuga superiore a quella della luce. In particolare si chiesero quale potesse essere il raggio $R$ di una stella di massa $M$ fissata la cui velocità di fuga fosse pari a quella della luce $c$ 1.
Tenendo conto della legge di conservazione dell’energia meccanica totale, si ricava: \[ \frac{1}{2} mv_f^2-G \frac{mM}{R}=0 \]
Da qui si può di conseguenza ricavare la velocità di fuga $v_f$: \[ v_f=\sqrt{\frac{2GM}{R}} \]
Dove $G$ e’ la costante di gravitazione universale. In questa formula il raggio $R$ della stella si trova al denominatore. Questo significa che se la massa della stella rimane costante mentre il suo raggio diminuisce (dato che la stella si contrae) la velocità di fuga aumenta. Con il diminuire del raggio, la velocità di fuga può aumentare fino a superare la velocità della luce nel vuoto $c$. Dato che secondo la relatività generale, niente può avere una velocità superiore a questo valore, è impossibile che un qualsiasi oggetto, anche un raggio di luce, possa allontanarsi da questa stella. Il valore critico del raggio $R$ per il quale la velocità di fuga diventa uguale alla velocità della luce nel vuoto lo calcolò esattamente nel 1916 Karl Schwarzschild, da cui ha preso il nome. Imponendo allora $v_f = c$ e $R = R_S$, si ricava:
\[ c^2=\frac {2GM}{R_S}
\]
da cui: \[ R_S=\frac{2GM}{c^2} \]
Queste stelle all’inizio vennero chiamate dark star, ma in seguito allo sviluppo della teoria ondulatoria e corpuscolare della luce il loro studio viene abbandonato quasi subito. Infatti la teoria ondulatoria e corpuscolare della luce stabilisce che i fotoni abbiano una massa nulla, quindi, secondo la teoria di Newton i fotoni non possono risentire dell’attrazione di alcuna stella, dunque le dark star non possono esistere.
Poi nel XX secolo la teoria dei buchi neri riaccese l’interesse degli scienziati, in seguito allo sviluppo di due potenti teorie che avrebbero riscritto la fisica macroscopica classica, la Relatività Ristretta e la Relatività Generale, e la fisica delle particelle, la Meccanica Quantistica. A questo punto, giusto per non generare equivoci, è bene sottolineare che col termine buco nero si intende una regione di spazio collassato su sé stesso. Quella parte di spazio ancora accessibile allo studio si chiama orizzonte degli eventi, sede di tutta una serie di fenomeni bizzarri che vanno dall’emissione spontanea di particelle (Radiazione di Hawking) fino a fenomeni di dilatazione temporale. La parte a noi sconosciuta e – per adesso – inconoscibile, è quello che rimane dell’oggetto (materia o radiazione) che ha prodotto lo spazio collassato: per la relatività generale è un punto geometrico di densità infinita chiamato singolarità. Dato che secondo la relatività generale niente può viaggiare più veloce della luce, dai buchi neri non sarebbe dovuto sfuggire niente, nemmeno un briciolo di radiazione termica. Per questa ragione all’inizio si era creduto che la temperatura dell’orizzonte degli eventi pari a zero Kelvin (ossia allo zero assoluto, $-273,15$ gradi centigradi). Questo assunto però era in contrasto con uno dei mostri sacri della fisica: il secondo principio della termodinamica.

Non importa se l’osservatore si avvicina a una stella o a un buco nero: egli percepirà la stessa curvatura nello spazio dovuta da un corpo di massa M.
Karl Schwarzschild, risolvendo le equazioni di Einstein (il campo gravitazionale è determinato dalla distribuzione di materia e dice alla materia come muoversi) in un caso molto particolare di perfetta simmetria sferica dello spazio-tempo, trovò una coincidenza molto interessante con la teoria newtoniana: se una stella di massa $M$ si contrae fino al raggio di Schwarzschild, il tempo sulla sua superficie si ferma e la luce che parte da quest’ultima subite un redshift infinito per cui non può raggiungere nessun osservatore al di fuori della stella. Cosa succede se il raggio della stella diventasse ancora più piccolo è ancora tema di dibattito. La relatività generale di Einstein non pone limiti al collasso della materia verso un punto di densità infinita. Per questo caso venne coniato il termine di singolarità di Schwarzschild, ma questa ipotesi fu accolta con grande scetticismo dalla comunità scientifica, oltre che dallo stesso Schwarzschild, convinti del fatto che la natura avrebbe trovato un modo per impedire simile ipotesi Grazie a una maggiore conoscenza e comprensione dei fenomeni fisici che avvengono all’interno delle stelle, tra gli anni Trenta e Cinquanta si arrivò alla conclusione che l’ipotesi della singolarità era reale e che la relatività generale non aveva alcun problema con la materia concentrata entro il raggio di Schwarzschild, anzi essa era in grado di spiegare chiaramente cosa succedeva fino all’orizzonte degli eventi: materia e luce intrappolate al suo interno e senza possibilità alcuna di uscire: una regione dello spazio-tempo che non può comunicare con il resto dell’universo. Il termine buco nero venne introdotto da Wheeler alla fine degli anni Sessanta, quando l’importanza fisica di tali oggetti era oramai chiara alla maggior parte dei fisici teorici e a gran parte degli astrofisici. Molti furono gli esperimenti compiuti per la ricerca di buchi neri e in effetti i telescopi furono in grado di rilevare dei candidati sempre più promettenti, anche se ancora oggi l’osservazione certa di un buco nero non sia stata confermata in modo assoluto. Ma sono rimasti in pochi a dubitare della loro esistenza. Negli stessi anni gli strumenti matematici impiegati dalla relatività generale furono notevolmente ampliati, comprendendo meglio i limiti di tale teoria. Le equazioni di Einstein vennero risolte sotto ipotesi meno restrittive di quelle di Schwarzschild insieme ad altri risultati. Grazie al contributo di numerosi teorici della relatività generale emersero quattro leggi fondamentali che regolano la meccanica dei buchi neri e presentano una straordinaria somiglianza formale con i principi della termodinamica. Inizialmente tale somiglianza venne considerata una pura coincidenza, a causa di evidenti incompatibilità tra le variabili che determinano la meccanica di un buco nero e le variabili termodinamiche a cui dovrebbero corrispondere.
La termodinamica dei buchi neri
Secondo Hawking non vi è alcun pericolo di perdere la popolazione di buchi neri nel nostro universo. Attualmente la radiazione di Hawking avrebbe un effetto rilevante solo sui buchi neri di piccola massa. 2. Questo perché la temperatura di un buco nero, cioè la radiazione di Hawking che emette il suo orizzonte degli eventi, deve superare la materia e l’energia che intercetta. Dato che la temperatura di un buco nero è inversamente proporzionale alla sua massa, allora con l’aumentare della massa la quantità di energia che riesce ad emettere diminuisce.
In questo modo, i buchi neri più massicci di quel limite, nati dal collasso di stelle massicce 3 4, presentano un’emissione di energia piuttosto bassa. E dato che ricevono continuamente luce dalle stelle, dalla radiazione cosmica di fondo e dalla materia che vi cade, è evidente che tali buchi neri non cessano di crescere.
Sarà solo quando in una data imprecisata nel futuro tutte le stelle si saranno spente, la poca materia ancora rimasta in un universo ormai freddo si troverà al di là della portata dei più grandi buchi neri ; quando la temperatura dell’universo sara’ inferiore a quella della radiazione di Hawking dei buchi neri neri che questi evaporeranno.
|
Nel 1974 il matematico inglese Stephen Hawking provò ad applicare la Meccanica Quantistica al concetto previsto dalla Relatività Generale conosciuto come Buco Nero. Questo dimostrò come i buchi neri non siano realmente neri, ma che emettano una temperatura di corpo nero inversamente proporzionale alla loro massa 5 6 [cite]10.1103/PhysRevD.23.287[/cite].
Il meccanismo della radiazione di Hawking introduce un paradosso insidioso e di difficile soluzione: la conservazione dell’informazione all’interno di un Buco Nero.
Detta così appare terribile, ma per la relatività generale non importa se la materia originale del buco nero sia materia o antimateria, di carica elettrica o di un sapore quantico particolare, potrebbe essere un astronauta, un libro o l’intera vostra collezione di CD; di tutto quello che supera l’orizzonte degli eventi se ne perde traccia e la radiazione di Hawking che ne esce non contiene alcuna informazione che consenta di risalire a ciò che era prima. Per la meccanica quantistica, lo stato di un sistema in qualsiasi momento è descritto da una funzione d’onda. Per la loro natura casuale, le particelle che compongono la radiazione di Hawking non hanno una funzione d’onda definita, ma solo una matrice di densità. Questo significa che la radiazione ha molte funzioni d’onda possibili, con una certa probabilità distribuita tra le particelle. Oltre all’incertezza usuale tipica della meccanica quantistica, nella radiazione si inserisce anche l’incertezza della funzione d’onda delle singole particelle: l’informazione è stata distrutta. Come Hawking ebbe a dire in proposito: “Non solo Dio gioca a dadi, ma a volte ci confonde gettandoli là dove non possono essere visti“.
 Al contrario, per la meccanica quantistica l’informazione non può essere distrutta. Qui ogni stato quantico di un insieme di due o più sistemi fisici, virtuali o reali, dipende dallo stato di quando ciascun sistema viene creato e si mantiene anche quando i singoli componenti dello stesso sistema sono spazialmente separati. Questo significa che se a una delle due particelle create insieme (un esempio classico sono un fascio di fotoni) viene imposto un particolare stato di polarizzazione esso si trasmette istantaneamente anche all’altra particella, senza alcuna limitazione spaziale 7. Quindi ogni modifica dello stato di una delle due particelle (o quella che cade oltre l’orizzonte degli eventi o quella che sfugge dal buco nero) si ripercuote anche sull’altra trasferendo informazione in un senso o nell’altro. Per comprendere meglio questo concetto è opportuno fare ricorso a un gedankenexperiment, un esperimento ideale tanto caro alla fisica teorica. Supponiamo due particelle entangled con spin $\nwarrow \hspace{0.75in} \nwarrow$ in prossimità dell’orizzonte degli eventi e una delle due cade nel buco nero mentre l’altra sfugge. Per il principio di equivalenza alla particella che cade non succede niente di particolare: lo spin $\nwarrow$ finisce oltre l’orizzonte degli eventi senza problemi. Ora all’esterno c’è una particella con spin $\nwarrow$ uguale a quella caduta all’interno, imbrigliata con questa; qualsiasi cambiamento di stato che una delle due subisce, si riflette istantaneamente attraverso l’orizzonte degli eventi.
Al contrario, per la meccanica quantistica l’informazione non può essere distrutta. Qui ogni stato quantico di un insieme di due o più sistemi fisici, virtuali o reali, dipende dallo stato di quando ciascun sistema viene creato e si mantiene anche quando i singoli componenti dello stesso sistema sono spazialmente separati. Questo significa che se a una delle due particelle create insieme (un esempio classico sono un fascio di fotoni) viene imposto un particolare stato di polarizzazione esso si trasmette istantaneamente anche all’altra particella, senza alcuna limitazione spaziale 7. Quindi ogni modifica dello stato di una delle due particelle (o quella che cade oltre l’orizzonte degli eventi o quella che sfugge dal buco nero) si ripercuote anche sull’altra trasferendo informazione in un senso o nell’altro. Per comprendere meglio questo concetto è opportuno fare ricorso a un gedankenexperiment, un esperimento ideale tanto caro alla fisica teorica. Supponiamo due particelle entangled con spin $\nwarrow \hspace{0.75in} \nwarrow$ in prossimità dell’orizzonte degli eventi e una delle due cade nel buco nero mentre l’altra sfugge. Per il principio di equivalenza alla particella che cade non succede niente di particolare: lo spin $\nwarrow$ finisce oltre l’orizzonte degli eventi senza problemi. Ora all’esterno c’è una particella con spin $\nwarrow$ uguale a quella caduta all’interno, imbrigliata con questa; qualsiasi cambiamento di stato che una delle due subisce, si riflette istantaneamente attraverso l’orizzonte degli eventi.
È evidente che questo è il nodo centrale di tutta la discussione: o si rinuncia alla trasmissione dello stato quantico delle particelle che oltrepassano l’orizzonte degli eventi oppure si rinuncia alla casualità della radiazione di Hawking. Un modo elegante per uscire da questa impasse consiste nel congelare l’informazione – e la rispettiva particella – proprio sull’orizzonte degli eventi, interrompendo così anche l’azione di entanglement che trasporta l’informazione di stato all’esterno. In questo modo, tutta l’informazione che precipita in un buco nero rimane congelata sul suo orizzonte degli eventi.
l’Effetto Unruh e il Principio Olografico

Per il Principio Olografico l’informazione può essere desunta dalle proprietà che proietta su una superficie, esattamente come le increspature nell’acqua si proiettano nei giochi di luce sul fondo di una piscina.
Nel 1993, Lenny Susskind ed altri [cite]http://arxiv.org/abs/hep-th/9306069[/cite][cite]http://arxiv.org/abs/hep-th/9308100[/cite] provano a definire una situazione non locale che non comprenda una perdita delle informazioni 8[cite]http://prd.aps.org/abstract/PRD/v14/i4/p870_1[/cite][cite]http://arxiv.org/abs/0710.5373[/cite]. Qui l’orizzonte degli eventi appare come una matrice di celle delle dimensioni di Plank, dove le informazioni di stato di ciò che cade nel buco nero vengono assorbite, mentre per il solito osservatore lontano pare che siano perse. Quindi i fenomeni entanglement non scompaiono ma vengono congelati sull’orizzonte degli eventi e l’informazione in realtà non è andata persa. Questa nuova interpretazione che voleva un orizzonte degli eventi caldo, all’inizio non era poi tanto convincente fino a che nel campo delle teorie quantistiche non apparvero le teorie delle stringhe e la teoria M, che avevano lo scopo di riunificare la meccanica quantistica con la gravità. Qui il contributo del fisico argentino Juan Maldacena fu determinante per comprendere meglio cos’è questo nuovo aspetto dell’orizzonte degli eventi caldo [cite]http://arxiv.org/abs/hep-th/9711200[/cite]. Anche alla luce della corrispondenza fra Spazio Anti de Sitter e Teoria di campo conforme (AdS / CFT) i risultati sono analoghi ai precedenti. Qui l’orizzonte degli eventi viene visto come un ologramma, una superficie che contiene tutte le informazione del buco nero 9. Così la corrispondenza AdS / CFT risolve, almeno in una certa misura, il paradosso dell’informazione dei buchi neri, mostrando come un buco nero possa evolvere coerente alla meccanica quantistica, senza alcuna perdita di informazioni.
Le ultime proposte di Hawking
 Nella sua ultima opera Hawking [cite]http://arxiv.org/abs/1401.5761[/cite] avanza delle critiche al concetto di firewall (come è stato ribattezzato l’effetto Unruh presso l’orizzonte degli eventi) trovando almeno tre grandi obiezioni a questo costrutto. Ha suggerito che occorre un cambio di passo (quello sì reale) nel modo di concepire i buchi neri pensandoli come oggetti finiti nel tempo, anche se lontanissimo, piuttosto che eterni e immutabili come spesso fatto finora. In quest’ottica anche il costrutto matematico che conosciamo come orizzonte degli eventi e descritto da Schwarzschild cambia di significato: è solo un limite del campo gravitazionale destinato a cambiare nel tempo, quindi si può definire come metastabile. Per questo Hawking lo definisce apparente, perché così appare all’osservatore per un tempo $T$. In questa nuova interpretazione il principio di unitarietà rimane intatto. La metrica di Kerr che può essere usata per descrivere un collasso di un buco nero reale indica che lo spazio oltre l’orizzonte degli eventi è essenzialmente caotico, quindi non occorre ricorrere al teorema olografico (e al firewall) per preservare l’informazione: questa passa nella radiazione di Hawking, ma talmente confusa da essere irriconoscibile. In questo modo la radiazione non appare più essere casuale come finora si era creduto, ma talmente caotica da sembrare tale.
Nella sua ultima opera Hawking [cite]http://arxiv.org/abs/1401.5761[/cite] avanza delle critiche al concetto di firewall (come è stato ribattezzato l’effetto Unruh presso l’orizzonte degli eventi) trovando almeno tre grandi obiezioni a questo costrutto. Ha suggerito che occorre un cambio di passo (quello sì reale) nel modo di concepire i buchi neri pensandoli come oggetti finiti nel tempo, anche se lontanissimo, piuttosto che eterni e immutabili come spesso fatto finora. In quest’ottica anche il costrutto matematico che conosciamo come orizzonte degli eventi e descritto da Schwarzschild cambia di significato: è solo un limite del campo gravitazionale destinato a cambiare nel tempo, quindi si può definire come metastabile. Per questo Hawking lo definisce apparente, perché così appare all’osservatore per un tempo $T$. In questa nuova interpretazione il principio di unitarietà rimane intatto. La metrica di Kerr che può essere usata per descrivere un collasso di un buco nero reale indica che lo spazio oltre l’orizzonte degli eventi è essenzialmente caotico, quindi non occorre ricorrere al teorema olografico (e al firewall) per preservare l’informazione: questa passa nella radiazione di Hawking, ma talmente confusa da essere irriconoscibile. In questo modo la radiazione non appare più essere casuale come finora si era creduto, ma talmente caotica da sembrare tale.
Quindi interpretare il pensiero di Hawking che chiede un nuovo approccio sui buchi neri come un rifiuto a questi è solo buttarla in caciara. I buchi esattamente neri non lo sono mai stati, e lo si sapeva dal 1974. Adesso sappiamo che l’orizzonte eventuale dura solo un tempo finito, e anche questa appare come la scoperta dell’acqua calda.
Note:
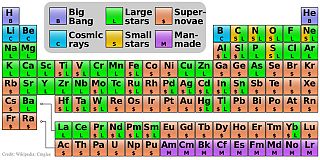 Sorgente: APOD: 25 gennaio 2016 – Where Your Elements Came From
Sorgente: APOD: 25 gennaio 2016 – Where Your Elements Came From