Categoria: Cosmologia

Nessun commento

Un’indagine astrochimica e narrativa sulla cometa 3I/ATLAS

Citazione

  di , , ,

All’inizio ero piuttosto scettico di parlare di 3I/ATLAS. Non perché non fosse interessante, ma per non aggiungermi al coro delle banalità scritte un po’ ovunque su questa cometa. Ma poi, di fronte alle tante corbellerie da Fine del Mondo che ho letto, mi sono deciso a scrivere anche la mia. Magari anch’essa una corbelleria, ma senz’altro più esotica e affascinante.

\(Ni\left( CO \right)_{4}\): la firma chimica di un viaggiatore interstellare

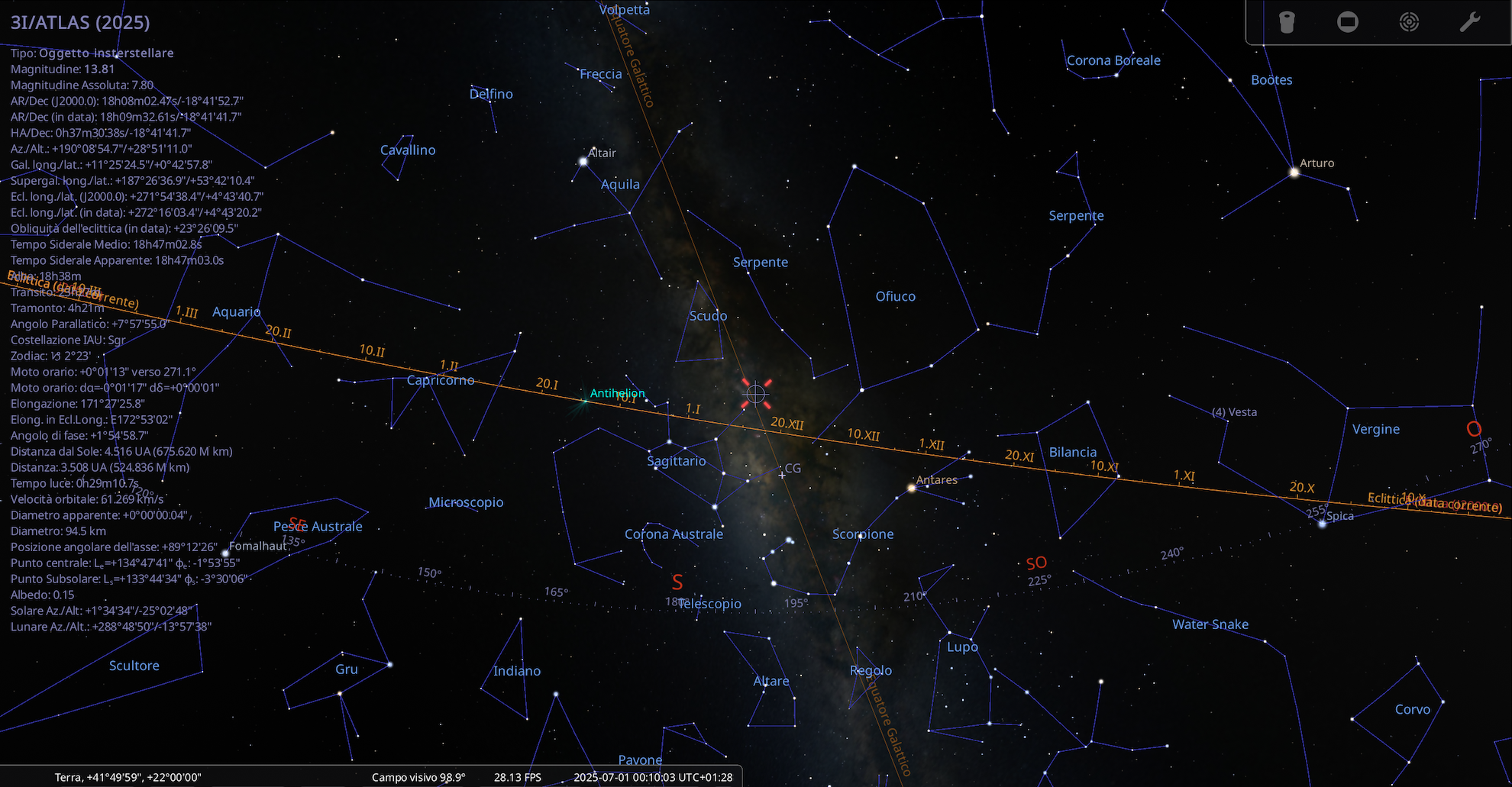La C/2025 N1 (3I/ATLAS) non è una comune cometa come quelle che di solito precipitano verso il Sole provenienti dalla Nube di Oort, La sua non è un’orbita ellittica e neppure parabolica. È iperbolica con una eccentricità notevole: \(e ~ 6.13±0.02\). L’immagine qui a fianco mostra il punto d’ingresso di 3I/ATLAS nel Sistema Solare il giorno della sua scoperta. L’oggetto cometario è arrivato nel nostro Sistema Solare poco sopra il piano dell’eclittica dalle regioni più dense della Galassia: tra il Sagittario e il Serpente, poco sotto lo Scudo. Le prime stime della sua età sono strabilianti: 7.8 miliardi di anni, una volta e mezzo quella del Sole e meno della metà dell’Universo!
L’età avanzata di un oggetto che proviene dal bulge galattico potrebbe far pensare che in qualche modo la sua provenienza sia quella. Io penso di no.
La velocità d’ingresso nel Sistema Solare era alta \(~58\;km/s \).
Ora, arrotondando per eccesso a 60 e considerano “solo” 7 miliardi di anni di moto rettilineo uniforme \(Spazio = Velocità \times  Tempo\),
\[60\ km/s\times 2.209032 \times10 ^{17} =1.33 \times10^{19} \ km\]
ovvero ~ 1.4 milioni di anni luce (ovviamente questo è un esercizio concettuale: nessun oggetto mantiene velocità costante per miliardi di anni dentro un ambiente dinamico come una galassia).
Ma  tra il Sistema Solare e il bulge galattico ci sono solo 26 mila anni luce, quindi qualcosa non torna con 3I/ATLAS. Come può essere così antico e veloce? Se l’età è giusta, allora è la velocità è l’unica cosa che può essere cambiata, così come la traiettoria.
Questo significa che 3I/ATLAS potrebbe provenire da molto più lontano, non dal bulge magari, ma da regioni esterne alla Galassia o addirittura da un’altra galassia.
3I/ATLAS potrebbe essere un planetesimo appartenuto a una stella di Popolazione II di una galassia satellite poi cannibalizzata o di un ammasso globulare molto antico distrutto dalle forze mareali del bulge galattico circa 8 miliardi di anni fa. Questa ipotesi può facilmente spiegare parametri come l’elevatata eccentricità,  l’orbita retrograda e l’elevata velocità iperbolica. Infatti, i valori mostrati da 3I/ATLAS sono decisamente troppo alti per un oggetto espulso da un sistema planetario appartenente alla Via Lattea e troppo bassi per un oggetto extragalattico. Ma perfettamente compatibili con un oggetto espulso durante una fusione galattica.
La Via Lattea ha inglobato diverse galassie nane nel corso della sua evoluzione, come la SagDEG (Sagittarius Dwarf Elliptical Galaxy) [1] e la Gaia-Enceladus [2]. Durante l’interazione mareale tra la galassia nana e la Via Lattea, le forze di marea e incontri ravvicinati con stelle massicce potrebbero aver espulso oggetti minori come 3I/ATLAS. Tramite questo meccanismo l’oggetto cometario avrebbe acquisito una velocità di fuga sufficiente a lasciarsi alle spalle il suo sistema d’origine, ma non la galassia ospite. Dopo la disgregazione della galassia nana, l’oggetto avrebbe vagato nel medio interstellare galattico, seguendo un’orbita caotica, fino a incrociare il Sistema Solare. Se 3I/ATLAS provenisse da una di queste galassie, la sua velocità di 68 km/s e la sua orbita iperbolica sarebbero il risultato di un’interazione dinamica antica, avvenuta miliardi di anni fa.

Ovviamente questa non è l’unica ipotesi, ma è una delle più affascinanti perché collega la cometa a eventi galattici antichi e a dinamiche cosmiche su scala galattica.

L’enigma chimico: nichel tetracarbonile

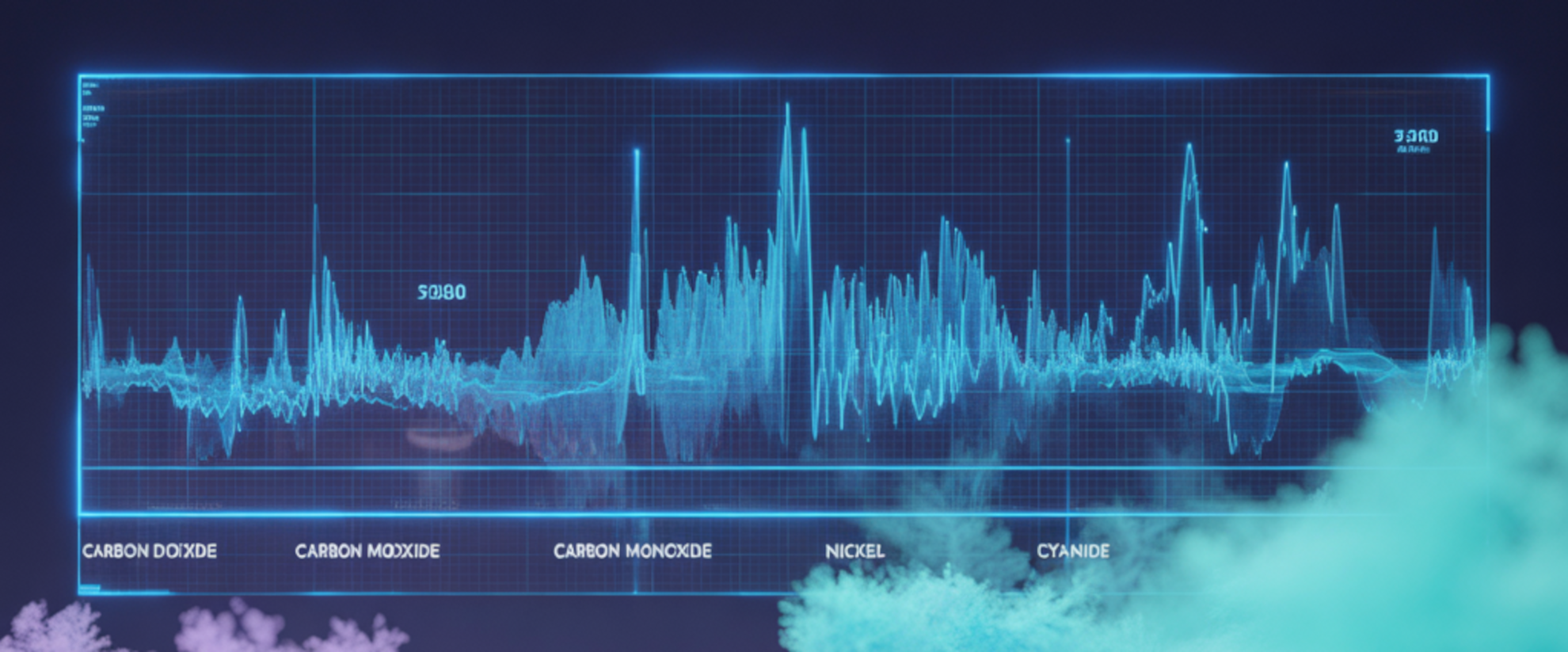
Tra le righe di emissione del monossido di carbonio e il cianuro (quasi assente) c’è una importante riga che appartiene al nichel, che in 3I/ATLAS è molto più abbondante del ferro.

La 3I/ATLAS ha mostrato una combinazione di firme chimiche mai osservate prima: un rapporto \(CO_{2}/H_{2}O\;\text{di}\;19.55:1\), emissioni intense di nickel senza tracce di ferro, e una dinamica che lo colloca tra gli oggetti più energetici mai entrati nel Sistema Solare.
I primi segni tipici di attività cometaria sono stati osservati quando l’oggetto interstellare era a circa 3 AU dal Sole, il che non è insolito per quella distanza. Era ossidrile (\(OH\)) prodotto dalla fotodissociazione ultravioletta delle molecole d’acqua in ragione di circa 40 kg/sec (stechiometricamente circa 88 kg di acqua per secondo). Ma la temperatura superficiale della cometa a quella distanza è di circa 100-120 K (-173°C a -153°C), calcolata con la legge di Stefan-Boltzmann \(\left( T\approx \left( S/ \sigma \right)^\frac{1}{4}\right)\), dove \(S\) è la costante solare ridotta a 162 W/m² a 2,9 UA). Questo significa che in quella regione dello spazio è ancora troppo freddo per la sublimazione diretta del ghiaccio d’acqua, che richiede almeno 150-200 K. Ma potrebbe essere in gioco un altro meccanismo di sublimazione indiretto: piccoli grani di ghiaccio d’acqua, espulsi dalla sublimazione di ghiaccio di \(CO\) o \(CO_{₂}\) (più volatili), vengano dissociati dalla radiazione UV solare a 4.000-10.000 km dal nucleo.

La cosa più eccitante è che lo spettro della cometa a quella distanza mostra anche una grande firma legata al nichel (\(Ni \;\text{I}\)) ma non al ferro, comunemente associato a questo elemento. Il nichel atomico gassoso è stato trovato nella coma di 3I/ATLAS nel agosto scorso dal telescopio Keck II a una distanza di ~3.8 UA dal Sole.
Una plausibile spiegazione è che sia il risultato della fotodissociazione ultravioletta del nichel tetracarbonile \(Ni\left( CO \right)_{4}\)- una sostanza che sulla Terra usiamo in industria ma che nello spazio ancora non è mai stata osservata direttamente, ma solo ipotizzata [3], [4].
il nichel tetracarbonile è un complesso organometallico che si decompone facilmente col calore. la sua temperatura di fusione è di 248 K. Ma come può essersi formato questo complesso? Ce lo spiega questo studio [5] pubblicato su ResearchGate, ed è molto intrigante.

L’ipotesi in questo articolo

 

Una plausibile immagine della superficie di 3I/ATLAS immaginata da me e realizzata dalla AI Grok 3.

Immaginiamo un planetesimo di ghiaccio che orbita nella nube di Oort attorno a una gigante rossa AGB 1 di Pop. II di una antica galassia satellite della Via Lattea. Una supergigante col rapporto \(C/O\gt 1\) e venti stellari ricchi di radicali \(C, C_{2}, CN\). In un ambiente così ricco di carbonio, qualunque metallo che condensa interagisce con superfici carboniose.
E il nichel è proprio uno di quei metalli di transizione capaci di adsorbire il carbonio e catalizzare la sua polimerizzazione e altri processi complessi. Questo non è un dettaglio marginale: è la base della chimica industriale del carbonio. La chimica del tetracarbonile di nickel è sorprendentemente “facile” se si hanno le condizioni giuste:

  • \(Ni\) metallico non ossidato o \(Ni^{0}\)
  • \(CO\) in grande abbondanza
  • basse temperature (50–200 K)
  • pressioni moderate (10⁻⁶–10⁻³ bar)
  • assenza di ossigeno libero

Tutte queste sono proprio le condizioni del vento di una stella asintotica ricca di carbonio e della successiva fase di raffreddamento dei grani. La formazione del nichel tetracarbonile diventa spontanea quando la temperatura dello spazio scende sotto i 200 K.

\[Ni^0 + 4\; CO\to Ni\left( CO \right)_{4}\]

È una reazione esotermica e spontanea, favorita dalle basse temperature e dall’eccesso di \(CO\). In pratica è la medesima reazione che Mond scoprì nel 1890, e che ancora oggi si usa industrialmente per purificare il nickel, solo che in questo caso siamo su scala stellare.
Riassumendo: il vento stellare di una gigante asintotica può essere riassunto in due momenti. Una fase calda (1300-1500 K) in cui avviene la condensazione dei solfuri di nichel (\(NiS, Ni_{3}S_{2}\)) e agglomerati di nichel non ossidato. E una fase fredda (200 > 50 K),m in cui il nichel non ossidato e il monossido di carbonio sono liberi di interagire. Il vento stellare si espande, si raffredda, e gli agglomerati metallici vengono carbonilati 2.

Il processo-s genera elementi pesanti catturando neutroni lentamente, consentendo ai nuclei instabili di decadere in forme stabili prima della successiva cattura. Questo meccanismo incontra due limiti naturali: il Bismuto-209 (209Bi), l’elemento stabile più pesante che il processo-s può produrre direttamente, il quale catturando un neutrone diventa 210Bi, instabile; e la “barriera” del Piombo-208 (208Pb). Il 210Bi decade in circa cinque giorni a Piombo-210 (210Pb), che attraverso successive catture di neutroni si trasforma in una catena stabile fino a Piombo-206, Piombo-207 e infine Piombo-208. Quest’ultimo, caratterizzato da un nucleo doppiamente magico, è estremamente stabile e poco reattivo ai neutroni aggiuntivi. In conclusione, il processo-s arricchisce le stelle soprattutto di 208Pb e, in misura minore, di 209Bi, che attraverso il decadimento contribuisce ulteriormente all’accumulo di 208Pb come prodotto finale.

Ma rimane un altro aspetto affascinante delle giganti asintotiche: i loro brevi ma potentissimi flash dell’elio 3; impulsi termici brevi ma potentissimi in cui il guscio dell’elio si accende violentemente, generando temperature di \(1-3 \times10^8 \;K\). Durante questi parossismi si ha una produzione massiccia di neutroni tramite la reazione \(^{13}C\left( \alpha,n \right)^{16}O\) 4.
Nel modello proposto da Young si calcola che ogni flash dell’elio raddoppi il rapporto \(Ni/Fe\) proprio per cattura neutronica (per ex. 6 flash, \(\to2^{6}\) = 64 volte più nichel del ferro. Ma questo non basta. Il nichel tende a formare solfuri volatili come ho precedentemente descritto, mentre il ferro invece si lega di più con i silicati e ossidi refrattari (olivine, pirosseni, \(FeO\)). E nella fase calda dei venti stellari, il nichel condensa con una efficienza attorno al 90% contro il 10% del ferro. Questo si traduce in un altro arricchimento del nichel a distanza molto maggiori della stella di circa 9 volte.
Combinando i due fattori, nucleosintesi e condensazione, e le debite correzioni al ribasso prudenziali, diciamo un efficienza dell’8%,  si ottiene:
\[Ni/Fe \approx64\times9\times0.08 \approx 46\]
un valore praticamente identico al limite osservato in 3I/ATLAS (Ni/Fe > 46). Almeno finché la 3I/ATLAS era a una distanza eliocentrica di 2,7 UA.

Poi a una distanza eliocentrica di 2.6-2-5 UA ecco comparire la riga spettroscopica del \(Fe \;\text{I}\) 5. Tra i 2.6 e 2 UA il rapporto \(Ni/Fe\) crolla e a distanze ancora inferiori tale rapporto diventa praticamente uguale a quello di una comune cometa del Sistema Solare.
Il concetto è molto semplice ed elegante [6]:
il \(Ni\left( CO \right)_{4}\) sublima molto prima (3,5-4 UA) del \(Fe\left( CO \right)_{5}\) ( <2,6UA).
Per questo si è notata prima la grande presenza del nichel I e poi del ferro I. È un comportamento puramente termico che però non contraddice quanto finora detto sull’abbondanza del nichel primordiale nella cometa. In sostanza si tratta di un processo evolutiv0 dipendente dalla distanza dal Sole, lo straordinario e mutevole rapporto \(Ni/Fe\) che stiamo osservando.

Conclusione

Noi osserviamo unicamente la chioma di 3I/ATLAS, non il suo nucleo. Ma dal modo in cui si evolve il rapporto \(Ni/Fe\) si può intuire l’origine della cometa, che si è fissata approssimativamente tra i 7 e 11 miliardi di anni fa in orbita  intorno a una gigante rossa asintotica di una galassia assorbita dalla Via Lattea, in un’area molto ricca di nichel e povera di ferro.
Io non credo a speculazioni di artefatti alieni e altre bischerate. Ogni cometa naturale ha movimenti non gravitazionali dipendenti dal criovulcanismo. 3I/ATLAS ha avuto 8 miliardi di anni di vuoto interstellare per accumulare ghiaccio che si è poi degradato grazie ai raggi cosmici. Per me è un planetesimo ricoperto di ghiaccio sporco che ci racconta una storia ben più intrigante di una mistica nave ‘liena. Con buona pace a chi ancora a quella strampalata ipotesi vuol ancora credere.

Cieli sereni

 

 

Nessun commento

VLTI (Gravity) registra la prima atmosfera extrasolare

  di , ,

HR8799. Una stella distante 129 anni luce, è la prima ad ospitare un pianeta di cui si sia osservata direttamente l’atmosfera!

Sono passati appena 40 anni da quando fu accertata l’esistenza dei pianeti attorno alle altre stelle; non che vi fossero dubbi al riguardo ma si riteneva che dimostrarne l’esistenza e perfino scrutarne qualcuno — come poi è stato fatto — fosse impossibile. E invece … eccoci qua!
Sfruttando l’ eccezionale apertura interferometrica di ben 100 metri (vedi nota a piè di pagina), gli astronomi sono riusciti a ricavare lo spettro dell’atmosfera di HR 8799 e, uno dei quattro pianeti di una stella molto giovane — appena una trentina di milioni di anni — di classe F0, distante appena 129 anni luce [7]. Il corpo celeste è un gioviano caldo, con una massa superiore di circa 10 volte quella di Giove ed è altrettanto giovane quanto la sua stella. Questa è una fortuna, perché permetterà in seguito di studiare nel dettaglio la sua evoluzione.
Comunque intanto sono stati raggiunti, e superati, diversi traguardi: il primo, e sicuramente il più importante, riguarda la capacità tecnologica di riuscire ad osservare finalmente l’atmosfera di un esopianeta, ossia di un mondo che non appartiene al nostro sistema solare; il secondo è che quell’atmosfera non è esattamente come i modelli standard delle atmosfere planetarie descrivono. E questo spingerà senz’altro gli astronomi a cercare e studiare altre esoatmosfere per cercare di comprenderne meglio i meccanismi. Intanto vi invito a consultare i link a fine articolo per vedere i risultati scientifici.
Questo è il link al comunicato ufficiale dell’ESO

[video_lightbox_youtube video_id=”uqdFCKSOJiY&rel=false” auto_thumb=”1″ width=”800″ height=”450″ auto_thumb=”1″]

 

Note:

 

Schizzo della disposizione dell’interferometro del VLT. La luce da un oggetto celeste distante entra in due dei telescopi del VLT e viene riflessa dai vari specchi nel tunnel interferometrico, al di sotto della piattaforma di osservazione sulla cima del Paranal. Due linee di ritardo con carrelli mobili correggono in continuazione la lunghezza dei cammini in modo che i due fasci interferiscano costruttivamente e producano frange di interferenza nel fuoco interferometrico in laboratorio.

L’Interferometria viene usata da decenni nel campo delle onde radio, dove si possono ottenere immagini con strumenti virtuali pari quasi al diametro terrestre, Il principio di funzionamento di un apparato interferometrico si basa sulla sovrapposizione in fase di due o più segnali coerenti allo scopo di esaltarne il segnale; per ottenere questo effetto però la differenza tra i cammini ottici dei fasci stessi deve rimanere inferiore ad un decimo della loro lunghezza ottica. Ora, nella radioastronomia il margine è piccolo ma comunque ottenibile senza grosse difficoltà: a 21 cm di lunghezza d’onda — ossia quella dell’idrogeno interstellare — la tolleranza è di appena 2 cm; anche se questa è misurata su basi lunghe migliaia di chilometri (Very-Long-Baseline Interferometry). Ma ricorrendo a trucchi che prevedono l’uso combinato di orologi atomici locali e maser all’idrogeno, l’ostacolo è comunque facilmente risolvibile.
Ma questi non funzionano nell’interferometria ottica dove le fasi del segnale sono lunghe appena 1μm (ossia nel vicino infrarosso) e dove quindi la tolleranza richiesta deve essere ancora dieci volte più piccola, Questo risultato però è ottenibile facendo convergere i fuochi dei 4 telescopi del VLT in un unico punto avendo cura che tutti i segnali percorrano esattamente la stessa distanza. In questo modo, e sfruttando sapientemente le ottiche adattive dei telescopi, si può raggiungere l’incredibile risultato di avere una risoluzione pari a circa un millesimo di secondo d’arco a  1μm di lunghezza d’onda. Il che significa risolvere un oggetto grande appena un paio di metri sulla Luna!

Links

Nessun commento

Una possibile atmosfera protoplanetaria per PDS 70b

  di , ,

SPHERE (Spectro-Polarimetric High-contrast Exoplanet REsearch instrument) sta davvero rivoluzionando l’astrofisica. Adesso è possibile scrutare i pianeti intorno alle loro stelle e studiare perfino per sommi capi la loro probabile atmosfera attraverso l’analisi spettroscopica di quella debole luce riflessa. Un traguardo che fino a pochi anni fa era ritenuto impossibile e che invece oggi si avvera.
Già mi pare di sentire le critiche — stupide — di chi pensa che tutto questo non serva a niente. Le immagini spettroscopiche e termiche riprese da droni, aerei e satelliti permettono di studiare e identificare infezioni e parassiti nelle coltivazioni agricole ben prima che i segni siano visibili sul campo [8]. Le tecnologie e principi che consentono di scorgere altri pianeti sono le stesse degli strumenti che ci permettono di vivere meglio su questo sassolino sperduto nell’infinito cosmo.

La posizione nel cielo di PDS 70 (V* V1032 Cen), una stella di tipo T Tauri un po’ più piccola del Sole (0,82 M☉) a 370 a.l. dalla Terra.

A prima vista PDS 70 è soltanto una delle miriadi di stelline che un qualsiasi buon telescopio nell’emisfero australe permette di vedere. Ma  in realtà è molto di più: essa è una stella nata da pochissimo, appena tra i 6 e i 10 milioni di anni ed è abbastanza vicina da permettere di studiare cosa accade in quel particolare momento, ovvero come si forma un sistema planetario. 
Già nel 1992 i dati del satellite IRAS[9] suggerivano PDS 70 come candidata ospite di un disco planetario, poi scoperto nel 2006.
Nel 2012 la svolta:  una regione vuota a circa 65 U.A. dalla stella suggerivano che lì si stava forse formando un pianeta [10] tra le 30 e le 50 volte Giove.
Successive osservazioni [11] hanno rivisto e corretto le prime stime confermando però la presenza di strutture protoplanetarie multiple: intorno a quella debole stellina si stavano formando più pianeti!

Lo studio con SPHERE: PDS 70b

Questa immagine, catturata dallo strumento SPHERE installato sul VLT (Very Large Telescope) dell’ESO, è la prima chiara fotografia di un pianeta nel momento in cui si sta formando; in questo caso intorno alla stella nana PDS 70, nella costellazione australe del Centauro. Il pianeta si distingue nitidamente; è il punto brillante alla destra della stella adeguatamente oscurata da un coronografo, una maschera che blocca la luce accecante della sorgente principale. Credit: ESO/A. Müller et al.

Quindi questa è per sommi capi la storia di PDS 70, una stellina di classe spettrale K5-K7 12, distante appena 370 anni luce — praticamente dietro l’angolo — e molto giovane (a quell’epoca sulla Terra le prime scimmie antropomorfe si preparavano a conquistare il mondo: i nostri antenati).
E adesso, grazie allo strumento SPHERE installato sul VLT (Very Large Telescope) dell’ESO, è stato finalmente possibile osservare il primo pianeta mentre è ancora nella fase della sua formazione [12] e di distinguere spettroscopicamente la sua probabile atmosfera [13].
Il pianeta, chiamato PDS 70b, appare mentre si sta aprendo la strada nel disco primordiale di gas e polvere intorno alla giovanissima stella a circa 3 miliardi di chilometri da questa (circa 20 U.A.), più o meno la distanza che separa Urano dal Sole con un periodo orbitale di 119 anni. Data la distanza e il periodo di rivoluzione non è stato difficile risalire alla stima della sua massa, che appare così di circa 10 masse gioviane.

Atmosfera protoplanetaria

Lo spettro di PDS 70b alla base delle simulazioni della sua atmosfera. Per una migliore comprensione leggere lo studio al riferimento 6 di questo articolo.

Ma non solo.  Grazie a SPHERE è stato possibile intercettare lo spettro di PDS 70b — che appare decisamente rosso, e stimare così anche la sua temperatura: circa 1200 ± 200 gradi Kelvin. E sempre grazie allo spettro del protopianeta è stato possibile risalire attraverso modelli e simulazioni numeriche alla possibile atmosfera di  questo.

Conclusioni

Il primo esopianeta fu scoperto nel 1995, ossia più di vent’anni fa.  I primi esopianeti osservati erano enormi e di solito orbitavano attorno a stelle più piccole del Sole. Questo perché per gli strumenti di quell’epoca erano gli unici oggetti che era possibile intercettare con le osservazioni, tant’è che per un momento si credette che tutte le nostre teorie sulla formazione planetaria fossero sbagliate. Dopo arrivarono strumenti più sofisticati, pensati apposta per raccogliere l’immane sfida di osservare oggetti sempre più piccoli e più difficili da scrutare. E così anche le teorie sulla formazione planetaria partendo dalla frammentazione dei resti della nube che aveva generato la stella furono confermate. Oggi lo vediamo con PDS 70b grazie a strumenti sempre più sofisticati come SPHERE. Anche strumenti di calcolo  sempre più potenti permettono di risalire alla composizione chimica delle atmosfere esoplanetarie così come possiamo risalire alla composizione chimica delle nubi di Venere con un normale telescopio.
Tra vent’anni cosa potremmo scoprire partendo da queste premesse?

Nessun commento

Alba cosmica

  di ,

Appena tre  articoli fa avevo stimato in un paio di miliardi di anni a partire dal Big Bang l’intervallo di tempo ragionevole per il crearsi delle condizioni minime necessarie per lo sviluppo degli elementi chimici più pesanti dell’idrogeno (per gli astrofisici questi sono chiamati tutti metalli a prescindere del loro peso atomico) necessari alla vita come la conosciamo, che io per comodità qui su questo Blog ho sempre chiamato Vita con la maiuscola.
Ma forse mi sbagliavo, quelle condizioni potrebbero essersi sviluppate molto prima: almeno 2/3 di quel lasso di tempo: appena 250-500 milioni di anni dopo il Big Bang. Quella fu la prima, vera, alba del Cosmo? difficile dirlo per ora; certo è che la primissima generazione di stelle apparve molto, molto, presto.

Nella grande immagine a sinistra, le numerose galassie dell’ammasso galattico MACS J1149 + 2223. Le lenti gravitazionali del cluster hanno permesso di scoprire una galassia 15 volte più lontana: MACS 1149-JD. In alto a destra vediamo lo zoom della regione mentre MACS 1149-JD è in evidenza nel dettaglio in basso a destra. Credit: NASA / ESA / STScI / JHU

MACS1149-JD1 non è una galassia appena scoperta e nemmeno la più grande — è appena un centesimo della Via Lattea. Fu scoperta dai telescopi spaziali Hubble e Spitzer nel lontano 2012 grazie all’azione di  lensing gravitazionale mediato dall’ammasso di galassie MACS J1149.6+2223, nella costellazione del Leone. Ma è nota per essere tra le più distanti dell’Universo osservabile — ha un redshift \(z \) di 9.6. La luce che oggi osserviamo abbandonò quella lontana galassia circa 13.3 miliardi di anni fa, cioè circa 500 milioni di anni dopo il Big Bang ed è talmente stirata per effetto dell’espansione dell’Universo da essere visibile solo nell’infrarosso (redshift cosmologico).

Ma seppur notevole non è questa la notizia più clamorosa che coinvolge MACS1149-JD1 [14]: un team di astronomi hanno studiato la luce di questa minuscola e debolissima galassia con ALMA (Atacama Large Millimeter/submillimetr Array)  e il VLT (Very Large Telescope) dell’ESO scoprendo così in essa il debole segnale dell’ossigeno ionizzato. Questo significa che nei suoi 500 milioni di anni era lì esistita una primissima generazione di grandi stelle che alla fine del loro ciclo vitale avevano cosparso il cosmo con le loro ceneri ricche di elementi pesanti tra cui l’ossigeno.
Già nel 2016 ALMA aveva permesso di scoprire tracce di ossigeno ionizzato in un altro oggetto del profondo cielo, la galassia SDXF-NB1006-2 [15], distante 13.1 miliardi di anni luce. Anche se la quantità di ossigeno allora rivelata risultava essere circa 10 volte meno di quella presente attualmente nella nostra galassia, in linea con quanto ci suggeriscono le simulazioni, indicava anche che l’intensa radiazione ultravioletta di quelle lontane stelle stava ionizzando una enorme quantità di gas, ben più di quanto ci si aspetterebbe se  la quantità di polvere e di carbonio fosse in linea con le proporzioni osservate dell’ossigeno. In pratica non c’era per SDXF-NB1006-2 quell’estinzione della componente ultravioletta che ci si sarebbe aspettato.
Ora MACS1149-JD1, oltre a spostare ancora più indietro nel tempo la presenza di ossigeno nell’Universo e di conseguenza la generazione stellare che l’ha creato, potrebbe contribuire a spiegare se la carenza di polveri era una caratteristica di quella lontana epoca oppure no.

Nessun commento

SPHERE celesti

  di ,

Using the ESO’s SPHERE instrument at the Very Large Telescope, a team of astronomer observed the planetary disc surrounding the star RX J1615 which lies in the constellation of Scorpius, 600 light-years from Earth. The observations show a complex system of concentric rings surrounding the young star, forming a shape resembling a titanic version of the rings that encircle Saturn. Such an intricate sculpting of rings in a protoplanetary disc has only been imaged a handful of times before. The central part of the image appears dark because SPHERE blocks out the light from the brilliant central star to reveal the much fainter structures surrounding it.

Se poteste tornare alla lontana epoca della formazione del Sistema Solare, quasi  5 miliardi di anni fa, ecco cosa vedreste.
Questo è quello che invece vediamo noi oggi, qui sulla Terra, guardando verso  WRAY 15-1443 [16], una giovanissima (5-27 milioni di anni) stellina di classe K5 distante circa 600 anni luce. Essa è parte di un filamento di  materia nebulare nelle costellazioni australi del Lupo e lo Scorpione insieme a decine di  altre stelline altrettanto giovani. È il medesimo scenario che vide la nascita del nostro Sole.
Noi vediamo il disco protoplanetario ancora come è durante la formazione dei pianeti e prima che i venti stellari della fase T Tauri lo spazzassero via, È un disco caldissimo e denso, con una consistenza è una plasticità più simili alla melassa che alla polvere che siamo soliti vedere qui sulla Terra. Qui le onde di pressione e i fenomeni acustici giocano un ruolo fondamentale nella nascita dei protopianeti creando zone di più alta densità e altre più povere di materia. E questa immagine ce lo dimostra chiaramente.

SPHERE. Credit: ESO

Lo strumento di cattura della luce polarizzata ad alto contrasto SPHERE.

Credit: ESO

Se oggi quindi possiamo ben osservare i primi istanti della formazione di un sistema solare questo lo dobbiamo a SPHERE (Spectro-Polarimetric High-contrast Exoplanet REsearch instrument) [17] [18]: uno strumento concepito proprio per catturare l’immagine degli esopianeti e dei dischi protoplanetari come questo.
L’ostacolo principale per osservare direttamente un esopianeta lontano è che la luce della sua stella è così forte che sovrasta nettamente la luce riflessa di questo: un po’ come cercare di vedere una falena che vola intorno a un lampione da decine di chilometri di distanza. Lo SPHERE usa un coronografo per bloccare la regione centrale della stella per ridurne il bagliore, lo stesso principio per cui ci pariamo gli occhi dalla luce più intensa per scrutare meglio. E per restare nell’ambito degli esempi, quando indossiamo un paio di lenti polarizzate per guidare o andare sulla neve, lo facciamo perché ogni luce riflessa ha un suo piano di polarizzazione ben definito e solo quello; eliminandolo con gli occhiali questo non può più crearci fastidio. Ma SPHERE usa questo principio fisico al contrario: esalta la luce polarizzata su un piano specifico e solo quella, consentendoci così di vedere particolari che altrimenti non potremmo mai vedere.

HARPS. Credit: ESO

Lo strumento per il rilevamento delle velocità radiali HARPS.

Credit: ESO

Oggi grazie a SPHERE e al team che l’ha ideato e costruito la ricerca astrofisica europea può vantare anche questo tipo di osservazioni che si sarebbe supposto essere di dominio della sola astronomia spaziale. E invece strumenti come HARPS[19] e HARPS-N alle Canarie consentono di scoprire sempre nuovi pianeti extrasolari, e ora SPERE ci aiuta a vederne pure alcuni.

 

Nessun commento

L’effetto Shapiro e le teorie MOND

  di ,

Il 17 agosto del 2017 è uno spartiacque nella storia dell’astronomia, ma soprattutto della cosmologia. È un momento che potremmo paragonare alla scoperta dell’inconsistenza della teoria dell’Etere Luminifero o quella della fine dell’universo statico sia nel tempo che nello spazio. Ma comunque, è ingiusto adesso pensare che l’aver speso tempo ed energie a studiare e proporre teorie della gravitazione che andassero al di la della Relatività Generale sia stato inutile. In fondo anche l’opera di Einstein appariva inutile visto che già c’era la Teoria di Gravitazione di Newton e che pareva funzionare quasi alla perfezione. Il tempo speso a meditare cose nuove o a vedere cose vecchie con spirito nuovo non è tempo buttato ma il sale della scienza.
E a chi afferma che di scienza si debbano occupare esclusivamente gli accademici, vorrei ricordare Milton Humason, collaboratore di Edwin Hubble e che insieme al celebre astronomo scoprì l’espansione dell’Universo, frequentò la scuola fino a 14 anni; Michael Faraday, uno dei padri dell’elettromagnetismo, era nato poverissimo e divenne garzone di bottega a 13 anni, fino a che a 23 anni non divenne assistente e cameriere di un professore di chimica:  Sir Humphry Davy. E potrei continuare all’infinito: Guglielmo Marconi era un autodidatta, proprio come me; Konstantin Ciolkovski, uno dei padri del volo coi razzi, anche lui era un autodidatta.
La scienza non è di nessuno, è di tutta l’umanità e soprattutto, non ha caste.

La prima e indubbiamente più eclatante previsione della Relatività Generale di Einstein fu quella relativa alla deviazione della luce delle stelle in presenza di oggetti dalla massa così enorme da piegare letteralmente lo spazio.
La conferma del fenomeno la fornì nel 1920 l’astronomo inglese Sir Arthur Eddington quando pubblicò i risultati delle sue osservazioni svolte durante l’eclissi totale di Sole del 1919. Qui è la distorsione dello spazio-tempo causata da una grande massa a flettere il percorso di un raggio luminoso. È il principio su cui si basano le lenti gravitazionali che ci consentono di veder le altre galassie dietro alla linea di vista di una galassia più vicina.

L’effetto Shapiro

Ma non di meno, una distorsione dello spazio-tempo causata da una massa ha anche un altro importante, e soprattutto misurabile, effetto: un ritardo temporale, conosciuto come effetto Shapiro [20].
Quando un segnale luminoso (ad esempio un segnale radar) passa vicino ad una massa importante impiega un po ‘più di tempo per colpire il bersaglio e tornare indietro rispetto a quando la suddetta massa non è presente. Tale ritardo di tempo è prodotto dalla distorsione dello spazio che aumenta la lunghezza fisica del percorso. Questo non è l’effetto della dilatazione temporale dovuta al pozzo gravitazionale (redshift gravitazionale) e anche se spesso i due effetti sono confusi fra loro, è proprio un’altra cosa [21].

Una delle prime immagini di Doppler di Venere fatta con un interferometro radar, le antenne Haystack e Westford in tandem, nel 1967. Sono riconoscibili le regioni Alpha e Beta, e la complessità di quest’ultima. Tener conto dell’effetto Shapiro è stato fondamentale per ottenere questo risultato. Credit: Alan EE Rogers.

Quando negli anni ’60 furono esplorati gli altri pianeti come Venere e Mercurio coi radar dalla Terra, fu assai importante tenere conto dell’effetto Shapiro per ottenere le prime immagini del suolo di quei pianeti: il ritardo del segnale radio causato dalla massa del Sole era sì piccolo, appena 200 microsecondi per Venere,  ma importante.
Lo stesso discorso vale per ogni altro segnale luminoso che viaggia nell’Universo. Se idealmente depurassimo ogni segnale luminoso dai redshift gravitazionali, i moti intrinseci dovuti dalla sorgente e dall’osservatore e da quello dell’espansione universale, quel che rimane è il ritardo temporale causato dall’effetto Shapiro, che è espressione indiretta delle distorsioni dello spazio causate da tutta la massa cosmologica presente tra la sorgente e l’osservatore. La massa cosmologica in questo caso è intesa essere la somma della massa barionica più il contributo della materia oscura, rilevabile esclusivamente dalla distorsione della metrica spazio-tempo. La certezza che la distorsione dello spazio-tempo sia dovuta a entrambe le due componenti viene dalle analisi del confronto delle radiazioni elettromagnetiche e il flusso di neutrini rilevato nell’occasione della supernova SN1987A [22] e altri studi sulle pulsar millisecondo  [cite]https://arxiv.org/abs/1210.1167[/cite].

Ma torniamo per un attimo al magico anno 1915. Fino a quel momento si era pensato alla gravità come una forza che agisce istantaneamente tra due corpi [23]. Se il Sole fosse misteriosamente scomparso dal Sistema Solare, i pianeti avrebbero immediatamente preso a girovagare nello spazio per la tangente, in virtù del principio di conservazione della quantità di moto. Per la Relatività invece, la gravità è concepita come una distorsione dello spazio-tempo: l’orbita di un corpo appare ellittica perché lo spazio in cui esso si muove è curvo. Nel tal caso i pianeti avrebbero continuato a percorrere le loro orbite finché lo spazio-tempo per loro non si fosse disteso: per esempio per la Terra questo accadrebbe dopo soli 500 secondi, per Giove dopo 43 minuti. Questo perché le le distorsioni nella metrica dello spazio, come lo sono anche le onde gravitazionali, si muovono alla velocità della luce [1.  La simmetria di Lorentz implica che tutto ciò che non è dotato di massa si propaghi nel vuoto alla velocità della luce e questo vale anche per le onde. Tuttavia quando un mezzo è presente, questa simmetria viene violata spontaneamente e anche le velocità di propagazione possono essere diverse. Pertanto, in virtù di questo principio, nella Relatività Generale ogni alterazione dello spazio-tempo viaggia — nel vuoto —  alla massima velocità possibile per un’onda priva di massa: la velocità della luce \(c\). ] e che quindi risentono della presenza di tutto ciò che può alterare lo spazio, ossia di tutta la materia ordinaria e di quella che oggi etichettiamo come materia oscura.

Le teorie MOND

Le teorie MOND sono una classe di teorie che tentano di spiegare la curva di velocità delle galassie assumendo che le Leggi di Newton non siano corrette se interpretate su scala galattica.

Ogni tentativo di conciliare la Relatività Generale con la Meccanica Quantistica è finora sempre fallito. È però apparso evidente fin da subito che una Teoria del Tutto avrebbe richiesto di passare per una riscrittura del concetto di gravità, che per la Relatività Generale è intesa come una distorsione nella metrica spazio-tempo piuttosto che come particella. Negli anni sono state tentate vie come la Teoria delle Stringhe, le Teorie M-Brane, suggerito nuove forze intese come tensori metrici che modificano la geometria dello spazio-tempo su scala cosmologica e dimensioni extra nel tentativo di spiegare certe anomalie che apparivano dai dati raccolti da nuovi e sempre più raffinati strumenti e da nuove scoperte riguardanti concetti come la Materia Oscura [24], l’Inflazione  post Big Bang e l’Energia Oscura 1.
Però intanto anche i test finora proposti hanno sempre mostrato che la Relatività Generale non è affatto facile da sostituire. L’unica soluzione possibile pare essere quella in cui il formalismo della Relatività Generale appare come caso speciale in un nuovo schema più fondamentale della Gravità allo stesso modo in cui il formalismo della Gravità di Newton appare all’interno della Relatività Generale. 
Le teorie che tentano di spiegare la piattezza delle curve di rotazione delle galassie senza ricorrere a nuove forme di materia esotica sono conosciute come Teorie MOND (MOdified Newtonian Dynamics), dette anche emulatori di materia oscura. Per questa classe di teorie sono le leggi della gravitazione di Newton (e quindi per estensione anche la Relatività Generale) a essere in errore  quando si tratta di piccolissime accelerazioni su scala galattica e comunque molto al di sotto di quello che oggi possiamo sperimentare all’interno del Sistema Solare.

La rivoluzione delle onde gravitazionali

Per le Teorie MOND le onde gravitazionali (in viola) percorrerebbero geodetiche molto diverse rispetto alla loro controparte elettromagnetica (in giallo) in quanto l’effetto Shapiro è molto diverso. Credit: Il Poliedrico

Il 17 agosto scorso la scoperta del primo segnale gravitazionale associato a un evento visibile (GRB 170817A), una kilonova 2  fu una scoperta grandiosa. Essa permise di misurare esattamente l’intervallo tra due tipi molto diversi di emissioni dello stesso evento: l’onda gravitazionale e l’impulso gamma scaturiti entrambi dalla coalescenza di una coppia di stelle di neutroni. Il dato fu molto interessante:1,74 secondi tra l’arrivo del treno di onde gravitazionali e il primo impulso elettromagnetico gamma.
Un niente se paragonato alla scala della distanza percorsa, 130 milioni di anni luce. Inoltre la differenza temporale tra i due eventi non ha in sé niente di trascendentale; anzi. Le onde gravitazionali hanno avuto origine pochissimi istanti prima della coalescenza delle due stelle di neutroni, quando cioè i due oggetti stavano cadendo l’uno sull’altro nella loro danza cosmica sempre più vorticosa. L’impulso gamma invece si è generato al contatto, quando cioè i due oggetti sono diventati uno solo. Ecco spiegato il ritardo tra i due impulsi: il GW170817 e il GRB170817A. Questo ci dice che entrambi gli impulsi hanno percorso i 130 milioni di anni luce alla medesima velocità.
Per la Relatività Generale, sia le onde gravitazionali che le elettromagnetiche percorrono le stesse geodetiche, ossia affrontano lo stesso percorso attraverso lo spazio-tempo. Per le teorie MOND invece le geodetiche percorse dai due tipi di onde sarebbero state molto diverse. Questo avverrebbe perché per loro la forza gravitazionale è intesa agire in modo assai diverso, essendo per questa classe di teorie la curvatura di potenziale gravitazionale dovuta esclusivamente dalla materia barionica ordinaria, lasciando tutto il resto alla reinterpretazione della gravitazione. In altre parole in base alla loro interpretazione, non essendo più la gravità una costante, di conseguenza finirebbe per non esserlo neppure il percorso delle onde gravitazionali rispetto alla luce. Pertanto se fossero state in qualche modo vere le basi delle teorie MOND avremmo dovuto registrare l’arrivo delle onde gravitazionali dell’evento GW170817 centinaia di giorni prima dell’evento elettromagnetico GRB170817A (e ovviamente a questo punto anche gli eventi avrebbero avuto nomi diversi).

Con l’aver registrato la sostanziale contemporaneità dell’evento gravitazionale con quello elettromagnetico si ottiene un altro punto fermo a cui ogni altra teoria alternativa o successiva alla Relatività Generale — ad esempio una Teoria del Tutto — deve per forza soggiacere per essere coerente con l’Universo che osserviamo. Di fatto questa osservazione contraddice in pratica ogni teoria che cerca di spiegare gli effetti che oggi attribuiamo alla materia oscura con una modifica delle leggi di gravitazione. Ma non solo. Anche ogni altro tentativo di spiegazione dei fenomeni che oggi osserviamo e i modi con cui tentiamo di spiegare l’Universo e come esso è nato, dovranno tener conto anche di questo importante paletto. 

 

Nessun commento

Kilonova

  di ,

No, una kilonova non è è una nova che si vende al mercato un tanto al chilo come si fa con le aringhe. E neppure è una miniera d’oro come alcuni roboanti titoli delle scorse ore, quelle seguenti l’annuncio della scoperta della prima controparte ottica di una sorgente di onde gravitazionali — anche questo è un termine alquanto impreciso in quanto tutti gli oggetti dotati di una grande massa che si muovono nello spazio in qualche modo lo sono —  hanno cercato di sottolineare. È un altro tipo dei tanti eventi violenti dell’Universo, ma solo un migliaio di volte, da qui il nome appunto di kilonova, di una nova comune.

Rappresentazione artistica dei resti di una kilonova. In giallo il nome di alcuni degli elementi prodotti dalla sintesi per cattura neutronica veloce che popolano la nebulosa finale. Tra parentesi il loro numero atomico. Credit: Il Poliedrico

L’Universo è una fonte inesauribile di meraviglie e di cose altrettanto grandiose. Dal pacato vuoto intergalattico alle possenti forze di un buco nero, dal flebile canto dell’atomo di idrogeno al cozzare di galassie in un balletto che dura milioni di anni. E in mezzo a tutto questo ci sono miriadi di fenomeni che ancora ci sono per la gran parte ignoti e che soltanto negli ultimi anni con l’avvento delle tecnologie radio e satellitari abbiamo imparato a vedere.
Ora alla pletora di strumenti che usiamo per scrutare il cosmo se n’è aggiunto un altro: l’interferometria gravitazionale. Per ora sono soltanto tre strumenti, due negli USA, a Hanford, Washington, e a Livingston, Louisiana che formano il complesso interferometrico LIGO, e l’altro è Virgo, a Cascina (PI), frutto di una collaborazione italo-francese (ad appena 83 chilometri da dove sono ora).

Un po’ di storia

Ma partiamo dall’inizio, come piace a me.
I primi evidenti segni che qualcosa ancora mancava al quadro generale dell’Universo, era che nonostante fosse stato compreso come si formassero gli elementi più pesanti dell’idrogeno — quelli che gli astrofisici apostrofano come metalli: carbonio, ossigeno, ferro, uranio, etc. — [25] era comunque difficile comprendere le quantità relative di alcuni elementi più pesanti del ferro che, come ho narrato nello scorso articolo sulle supernove [26], non sono prodotti dalla normale attività di fusione nucleare di una stella ma per cattura neutronica quando questa esplode 1. Doveva esserci quindi qualche altro processo cosmico ancora sconosciuto che ricorresse alla cattura neutronica veloce (r-process) al di fuori delle supernove comuni per giustificarne le quantità osservate.
Intanto si erano scoperti anche i lampi di raggi gamma (Gamma Ray Burst o GRB), i più violenti fenomeni dell’intero Universo, capaci di sterilizzare interi mondi a una distanza di migliaia di anni luce [27].
Si è scoperto che questi eventi, che di solito durano da qualche secondo a qualche minuto mentre la loro energia luminosa decade verso frequenze più basse come raggi X, ultravioletto, visibile, etc., sono di solito associati a eventi di supernova mentre questa decade verso una stella di neutroni o un buco nero. I precursori più probabili per emettere un lampo gamma finale sono le stelle molto massicce come le Wolf-Rayet: \(\eta\) Carinae e WR 104 sono le nostre più vicine (entrambe tra i 7500 e gli 8200 anni luce, per nostra fortuna).
Ma ci sono anche GRB molto più rapidi, dell’ordine di un paio di secondi o meno. Questi sono difficili da spiegare con lo stesso meccanismo delle supernove, eppure sono capaci di rilasciare lo stesso energia sulla scala delle loro galassie ospiti nell’arco di pochissimi secondi. Una plausibile spiegazione a questi fenomeni parossistici arrivò nel 2007 coi lavori di  Benjamin P. Abbott del LIGO – Caltech [cite]https://arxiv.org/abs/0709.0766[/cite] che ipotizzò essere generati dalla fusione di due stelle di neutroni o tra una stella di neutroni e un buco nero.

Kilonova

Queste immagini furono scattate dal NASA Hubble Space Telescope il 13 giugno e poi il 3 luglio 2013 e rivelano un nuovo tipo di esplosione stellare prodotta dalla fusione di due oggetti compatti: due stelle di neutroni o una stella di neutroni e un buco nero. Credit: NASA, ESA, N. Tanvir (Università di Leicester) e A. Fruchter, Z. Levay (Space Telescope Science Institute), A. Levan (Università di Warwick)

Una teoria interessante che trovò la prima conferma quando il 3 giugno del 2013  il telescopio per raggi  gamma Swift intercettò un evento che durò poco meno di due secondi proveniente da una galassia a 4 miliardi di anni luce, GRB130603B. In seguito, il 13 giugno, l’Hubble Telescope registrò nello stesso posto una sorgente  infrarossa in decadimento. L’analisi spettrale della sorgente mostrava una inusuale abbondanza di elementi chimici più pesanti del ferro tipici di un processo di cattura neutronica rapida r-process 2 rispetto agli altri spettri usuali di supernova.
Quando due stelle di neutroni finiscono per fondersi parte della loro energia cinetica si disperde sotto forma di increspature dello spazio-tempo, ossia onde gravitazionali allo stesso modo del merging di due buchi neri come già VIGO era riuscito a rilevare in passato e a quelle rilevate col GW170817 [28]. Un’altra parte invece viene assorbita dai due oggetti che sì disintegrano disperdendo così una buona parte della loro massa. È qui, nel materiale espulso che avvengono le reazioni di cattura neutronica: in pratica un immenso guscio di neutroni ancora ad altissima densità e temperatura (\(\rho\) > 3 x1011 gm/cm3 e T > 9×109 K) in cui le reazioni di nucleogenesi fino ad allora inibite dalla possente gravità delle precedenti stelle di neutroni riprendono vigore [cite]https://arxiv.org/abs/1105.2453[/cite]. 
In una kilonova quindi il processo di nucleogenesi per cattura neutronica rapida pare essere la principale reazione nucleare presente. Tale reazione consente la formazione di nuovi elementi più pesanti del ferro, ed è pertanto una reazione che assorbe energia dal sistema (reazione endotermica), raffreddandolo. Per questo appare debole come flusso elettromagnetico, da un decimo a un centesimo rispetto a una normale supernova; una parte assai importante dell’energia viene assorbita dalla creazione di elementi pesanti attraverso l’unico processo possibile: la cattura nucleare di altri neutroni. Il raffreddamento del materiale eiettato aumenta in modo drammatico l’opacità dell stesso spostando di conseguenza l’emissione radiativa principale verso frequenze sempre più basse piuttosto in fretta. Per questo l’Hubble Telescope non poté che registrare che il 3 luglio 2013, dopo appena un mese dal lampo gamma GRB130603B, l’evento era quasi scomparso anche dalla banda dell’infrarosso.

Il processo-r

Il reazioni di nucleogenesi per cattura neutronica rapida che danno origine a nuclei atomici più pesanti del ferro (u > 55) sono endotermiche, assorbono cioè energia all’ambiente dove avvengono. In una supernova esse sono responsabili della perdita di equilibrio della stella che finisce così per esplodere. Dal momento dell’esplosione, la densità neutronica della stella decresce rapidamente così che queste reazioni cessano abbastanza in fretta.  Inoltre i processi di fotodisintegrazione causati dai fotoni più energetici che colpiscono i nuclei più instabili estinguono la produzione di atomi pesanti altrettanto rapidamente. 
Nel caso di fusione di due stelle di neutroni invece la densità energetica dei fotoni è alquanto minore mentre la densità dei neutroni liberati nell’evento è molto più grande rispetto a un normale evento di supernova di tipo II (T ≥ 1,2 x 109 K e nn > 1 x 1022 cm-3).  Qui processi di cattura neutronica sono molto più importanti e anche il decadimento beta che spinge i nuclei più instabili verso la formazione di atomi più stabili ha più tempo per prodursi prima che intervengano i processi di fotodisintegrazione. 
La sottrazione di energia dal sistema è anch’essa molto importante perché pone un limite minimo al di sotto del quale comunque le reazioni di cattura neutronica cessano. Una volta cessata la produzione di nuclidi instabili ricchi di neutroni, è il decadimento radioattivo di questi a dominare la scena della nebulosa creatasi dopo il merging dei due corpi originali.

Conclusioni

L’ultimo evento scoperto, GW170817 è il secondo caso ormai accertato di una kilonova.  La rilevazione delle onde gravitazionali prodotte durante l’evento di coalescenza fissa drammaticamente un limite alle masse delle stelle di neutroni coinvolte e questo permette così di studiare più in dettaglio questo genere di fenomeni e le reazioni nucleari che lo governano.
Un altro importante traguardo è stata la stima della differente velocità delle onde gravitazionali rispetto alle onde elettromagnetiche su un percorso di ben 130 milioni di anni luce: 1,7 secondi a vantaggio delle prime. Dal punto di vista cosmologico questo è un grande risultato che spazza via tante teorie che puntavano a modificare la gravità pur di eliminare il problema della materia oscura. Ma questo potrà essere argomento di un’altra storia.

Nessun commento

Le grandezze fisiche dei buchi neri

  di ,

La radiazione di Hawking

Credit: Il Poliedrico.

Come ho cercato di spiegare nelle puntate scorse dedicate ai buchi neri [cite]https://ilpoliedrico.com/2017/03/il-principio-olografico-dei-buchi-neri-lorizzonte-degli-eventi.html[/cite], questi curiosi oggetti hanno diverse peculiarità uniche definibili solo matematicamente.  
Sulla base della convinzione — corretta — che niente può viaggiare più veloce della luce si era supposto quindi che nulla potesse sfuggire da un buco nero. Tecnicamente è ancora corretto pensare questo, ma nel 1974 il cosmologo Stephen Hawking dimostrò che in realtà i buchi neri emettono una radiazione termica di corpo nero diversa da zero. Il ragionamento che è alla base di questa scoperta è che lo spazio non è mai esattamente vuoto ma ribolle di energia che si manifesta con la produzione spontanea di coppie di particelle e antiparticelle virtuali, ovvero che la loro esistenza è limitata dal Principio di Indeterminazione di Heisenberg [cite]https://ilpoliedrico.com/2016/07/zenone-olbers-lenergia-oscura-terza-parte.html[/cite].
Quando queste fluttuazioni del vuoto si manifestano in prossimità dell’orizzonte degli eventi di un buco nero può capitare che una coppia di particelle virtuali finisca oltre l’orizzonte (A nella figura); in tal caso l’equilibrio energetico complessivo del’universo e la massa/energia del buco nero non variano, come impone il Principio della Conservazione della massa/energia. Lo stesso ovviamente accade anche per le particelle virtuali che si annichiliscono spontaneamente nello spazio normale (scenario B nella figura). Ma può capitare che soltanto una di queste finisca oltre l’orizzonte degli eventi (vedi evento C);  questo scenario potrebbe far da principio supporre che esso violi il postulato precedente in quanto la particella che riesce a non finire oltre l’orizzonte degli eventi diviene una particella reale, ma in realtà non è così. La particella che cade nel buco nero è l’antiparticella di quella che sfugge, ossia possiede alcuni numeri quantici opposti rispetto ad essa. Questo non viola il Principio di Conservazione della massa/energia perché il buco nero acquista una particella opposta al resto dell’universo e la somma totale dell’energia rimane invariata. Ma se adesso nell’universo c’è la massa/energia di una particella in più allora significa che il processo iniziale sottrae la medesima quantità di massa/energia al buco nero. Per un ideale osservatore lontano la nuova particella appare provenire dal buco nero, ma in realtà essa ha origine nello spazio normale appena oltre l’orizzonte degli eventi.

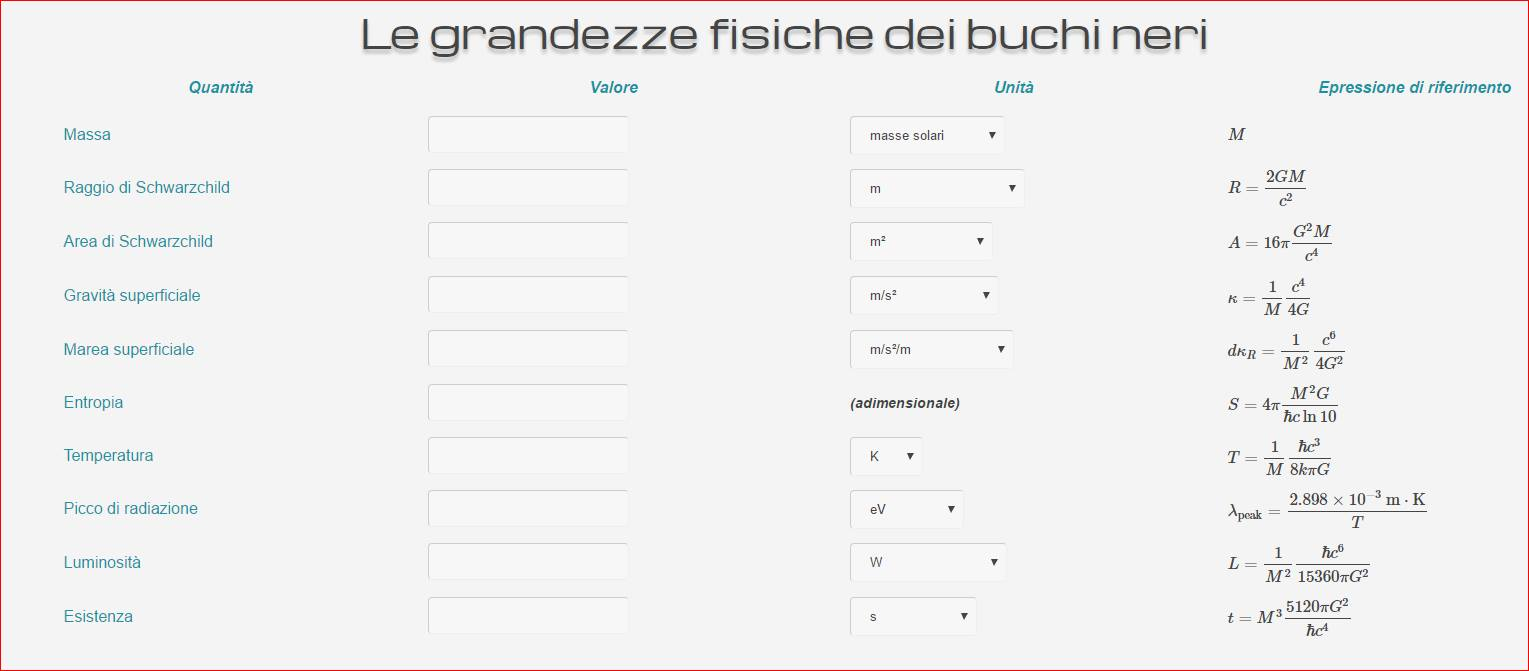[fancybox url=”https://ilpoliedrico.com/le-grandezze-fisiche-dei-buchi-neri” ][/fancybox]Cliccando sull’immagine qui sopra vi si aprirà una finestra su cui potete sbizzarrirvi a studiare alcune delle bizzarre  proprietà matematiche dei buchi neri.

Questa intuizione di Stephen Hawking, che ricordo ebbe origine anche dai lavori di due scienziati sovietici, Yakov Zeldovich e Alexei Starobinsky, che fin dagli inizi degli anni 70 del secolo scorso avevano ipotizzato la generazione di particelle attorno ai buchi neri rotanti (1973/74), dimostra che i buchi neri in effetti possano perdere massa tramite la radiazione che porta, appunto, il suo nome.
Quindi, in un certo senso i buchi neri non sono poi così neri.  Il lavoro di Hawking ha spinto altri cosmologi a studiare più in dettaglio i buchi neri fino a postulare le loro leggi termodinamiche [cite]https://ilpoliedrico.com/2017/03/il-principio-olografico-dei-buchi-neri-la-termodinamica.html[/cite], il noto Principio Olografico e altre bizzarre proprietà che in queste pagine posso solo elencare solo parzialmente. 

 Giocando con i calcoli

 Giostrando un po’ coi diversi parametri nella pagina che ho creato (è presente anche nel menù a discesa sotto la voce “Science”) si nota come i buchi neri siano ancora più strani di quel che si pensi.
Ad esempio, la temperatura di un buco nero, conseguenza della Radiazione di Hawking, è inversamente proporzionale alla sua massa ossia un buco nero piccolo irradia di più di uno di massa più grande.
L’attuale fondo di radiazione cosmica ha una temperatura di 2.72 kelvin; perché un buco nero sia termicamente rilevabile dovrebbe poter emettere a una temperatura appena superiore. Ma i numeri sono impietosi: un siffatto buco nero sarebbe grande appena 67μm, circa quanto lo spessore di un capello umano, e quindi — almeno con gli strumenti attuali — impossibile da rilevare direttamente.  
Un buco nero capace di emettere alla stessa temperatura del Sole, ovvero 5778 kelvin, sarebbe grande appena 30 nanometri, quanto cioè la giunzione di un transistor in un processore di qualche anno fa. Avrebbe ancora una vita molto lunga prima di evaporare, circa 2,5 x 1034 anni, comunque moltissime volte di più dell’età attuale dell’Universo.
Magari una civiltà avanzatissima potrebbe essere in grado di imbrigliare un micro buco nero ed avere così una fonte virtualmente infinita di energia.

Non voglio levarvi il divertimento di provare a fare nuove speculazioni con le cifre che si possono ricavare dalla tabella. Anzi vi invito a farlo e poi a condividerle nei commenti. 
Cieli sereni

Nessun commento

Il principio olografico dei buchi neri – L’orizzonte olografico

  di ,

I buchi neri sono un argomento molto complesso. Per descriverli compiutamente e raccontare del loro impatto sugli studi del cosmo non basterebbe una enciclopedia, figuriamoci le poche pagine di un blog. Parafrasando la celebre frase — forse apocrifa anch’essa come la celebre mela di Newton — del grande Galileo: “Eppur ci provo” …

[vrview img=”https://ilpoliedrico.com/wp-content/uploads/2017/03/p02rz7hw.png” stereo=”false”]
Volete fare un viaggio in prossimità dell’orizzonte degli eventi? Ecco una plausibile simulazione. Cliccate sulla figurina in basso a destra.

Senza ombra di dubbio i buchi neri sono tra gli oggetti astrofisici più noti e studiati nel dettaglio. Nessuno ha mai realmente visto un buco nero, ma grazie alla Relatività Generale se ne conoscono talmente bene gli effetti che esso ha sul tessuto dello spazio-tempo circostante che oggi è possibile cercare nel Cosmo i segni della loro presenza e descriverli graficamente.
Dai nuclei delle galassie AGN fino ai resti di stelle massicce collassate e ancora più giù fino agli ipotetici micro buchi neri formatisi col Big Bang, si può dire che non c’è quasi limite alle dimensioni che questi oggetti possono raggiungere [cite]https://arxiv.org/abs/astro-ph/9605152[/cite].

Il Principio Olografico


L’entropia (misura dell’informazione nascosta) di un buco nero, misurata in bit, è proporzionale all’area del suo orizzonte degli eventi misurata in unità di Planck
Jacob Bekenstein

Per comprendere l’interpretazione olografica dell’orizzonte degli eventi di un buco nero, occorre prima ripetere ciò che avevo accennato nella scorsa puntata, ossia se un buco nero distrugga o meno l’informazione riguardante tutto ciò che finisce oltre il suo orizzonte degli eventi — ricordo che questo è più un concetto matematico più che un oggetto tangibile.
Secondo Shannon i concetti di entropia e di informazione si equivalgono e, come anche Leonard Susskind ha ribadito, l’entropia non è altro che la misura delle informazioni nascoste, cioè quelle che a noi non sono note. Se infatti le conoscessimo potremmo ricostruire l’evento che le ha generate, come ad esempio possiamo risalire alla massa, traiettoria ed energia di una particella coinvolta in una collisione in una camera a bolle semplicemente ripercorrendo a ritroso la storia degli eventi che essa ha scatenato.

Il teorema della complementarietà dei buchi neri fu proposto da Susskind (anche questo concetto è mutuato da altre teorie, in questo caso dalla meccanica quantistica) per risolvere il paradosso dell'informazione perduta dentro un buco nero. Qui per l'osservatore A l'astronauta varcherebbe l'orizzonte degli eventi di un buco nero ma verrebbe distrutto mentre tutta la sua informazione verrebbe distribuita su tutta la superficie dell'orizzonte degli eventi. Invece per l'osservatore B oltre l'orizzonte o per lo stesso astronauta l'attraversamento dell'orizzonte avverrebbe senza particolari fenomeni di soglia, come già descritto nel primo articolo.

Il teorema della complementarietà dei buchi neri fu proposto da Susskind (anche questo concetto è mutuato da altre teorie, in questo caso dalla meccanica quantistica) per risolvere il paradosso dell’informazione perduta dentro un buco nero. Qui per l’osservatore A l’astronauta varcherebbe l’orizzonte degli eventi di un buco nero ma verrebbe distrutto mentre tutta la sua informazione verrebbe distribuita su tutta la superficie dell’orizzonte degli eventi. Invece per l’osservatore B oltre l’orizzonte o per lo stesso astronauta l’attraversamento dell’orizzonte avverrebbe senza particolari fenomeni di soglia, come già descritto nel primo articolo.

Come ho cercato di spiegare nelle precedenti puntate tutta l’entropia — o informazione nascosta equivalente — di un buco nero può solo risiedere sulla superficie degli eventi come microstati — o bit — grandi quanto il quadrato della più piccola unità di misura naturale, ossia la lunghezza di Plank 1. Questo significa che tutta l’informazione di tutto ciò che è, od è finito, oltre l’orizzonte degli eventi, è nascosta nella trama dell’orizzonte degli eventi stesso. Potessimo interpretare compiutamente questa informazione, idealmente potremmo risalire alla sua natura.
In base a questa interpretazione tutto ciò che è contenuto in una data regione di spazio può essere descritto dall’informazione confinata sul limite della stessa, così come la mia mano è descritta da ciò che di essa percepisco dalla superficie dello spazio che occupa.
In pratica quindi l’informazione tridimensionale di un qualsiasi oggetto è contenuta su una superficie bidimensionale, che nel caso dei buchi neri, è rappresentata dall’orizzonte degli eventi 2.
L’analogia col fenomeno a noi più familiare è quella dell’ologramma, dove tutte le informazioni spaziali riguardanti un oggetto tridimensionale qualsiasi sono impresse su una superficie bidimensionale. Osservando l’ologramma noi effettivamente percepiamo le tre dimensioni spaziali, possiamo ruotare l’immagine, osservarla da ogni sua parte etc., ma essa comunque trae origine dalle informazioni impresse su una superficie bidimensionale; la terza dimensione percepita emerge 3 dalla combinazione di tutte le informazioni lì racchiuse.

Conclusioni

Il Principio Olografico è questo: un modello matematico che tenta di conciliare la Termodinamica e la meccanica della Relatività Generale dei buchi neri, due leggi che finora si sono dimostrate universalmente esatte e che nel caso specifico dei buchi neri sembrano violarsi.
Questo modello è reso ancora più intrigante per le sue particolari previsioni teoriche: dalla validità della Teoria delle Stringhe alla Super Gravità Quantistica passando per le teorie MOND (Modified Newtonian Dynamics) che potrebbero addirittura dimostrare l’inesistenza della materia e dell’energia oscure.
Addirittura il Principio Olografico potrebbe essere usato per suggerire che l’intero nostro Universo è in realtà un buco nero provocato dal collasso di una stella di un superiore universo a cinque dimensioni, ci sono studi al riguardo [cite]https://www.scientificamerican.com/article/information-in-the-holographic-univ/[/cite] [cite]https://arxiv.org/abs/1309.1487[/cite].
Cercherò in futuro di trattare questi argomenti, sono molto intriganti.

Nessun commento

Il principio olografico dei buchi neri – La termodinamica

  di ,

Può suonare strano a dirsi, ma tutta l’energia che vediamo e che muove l’Universo, dalla rotazione delle galassie ai quasar, dalle stelle alle cellule di tutti gli esseri viventi e perfino quella immagazzinata nelle pile del vostro gadget elettronico preferito è nato col Big Bang. È solo questione di diluizioni, concentrazioni e trasformazioni di energia. Sì, trasformazioni; l’energia può essere trasformata da una forma all’altra con estrema facilità. La scienza che studia tali trasformazioni è la termodinamica. Per trasformarsi l’energia ha bisogno di differenza di potenziale, ossia una maggior concentrazione contrapposta a una minore concentrazione nella stessa forma. L’entropia non è altro che la misura della capacità che ha l’energia di decadere compiendo un lavoro fino a raggiungere di uno stato di equilibrio.

[virtual_slide_box id=”11″]
L’entropia statistica si fonda sulle probabilità delle posizioni delle molecole in uno spazio chiuso. Il II Principio della Termodinamica deriva dal fatto che le configurazioni ad alta entropia sono più probabili di quelle a bassa entropia.
L’esempio dei vasi comunicanti è un classico. Quando fra i due contenitori viene rimosso il tappo (blu), le molecole di un gas (rosse) saranno libere e si distribuiranno uniformemente in entrambi i contenitori compiendo un lavoro (il transito).
Quando la distribuzione sarà uniforme non potrà più esserci lavoro (equilibrio).

Nella termodinamica l’entropia è la misura delle capacità di un sistema fisico in grado di essere sede di trasformazioni spontanee. In altre parole essa indica la perdita di capacità a compiere un lavoro quando tali trasformazioni avvengono. Il valore dell’entropia cresce quando il sistema considerato man mano perde la capacità di compiere lavoro ed è massimo quando tutto il sistema è in condizioni di equilibrio.
La meccanica statistica ha poi reso lo stesso concetto, originariamente legato agli stati di non equilibrio di un sistema fisico chiuso, ancora più generale, associandolo anche alle probabilità degli stati — microstati 1 — in cui può trovarsi lo stesso sistema; da qui in poi si parla di grado di disordine di un sistema quale misura di indeterminazione, degrado o disordine di questo. Il classico esempio dei vasi comunicanti aiuta senz’altro a capire questo poi banale concetto. Ne potete vedere un esempio illustrato qui accanto.
Il legame fra l’entropia statistica e la teoria dell’informazione lo si deve a  Claude Shannon (il padre del termine bit e dell’uso della matematica binaria nei calcolatori) intorno agli anni quaranta del ‘900. Shannon notò che non c’era differenza tra il calcolo del livello di imprevedibilità di una sorgente di informazione e il calcolo dell’entropia di un sistema termodinamico.
Per esempio, una sequenza come ‘sssss‘ possiede uno stato altamente ordinato, di bassa entropia termodinamica. Una sequenza come ‘sasso‘ ha un grado di complessità superiore e e trasporta più informazioni ma ha anche un po’ di entropia in più, mentre ‘slurp‘ dimostra un ancora più alto grado di complessità, di informazione e di entropia perché contiene tutte lettere diseguali; noi le diamo un significato, è vero, ma se dovessimo basarci solo sulla frequenza con cui appaiono le singole lettere in una parola composta da cinque di esse, questa possiede la stessa entropia di “srplu“, che per noi non ha senso e diremmo che essa è una parola disordinata o degradata.
Nell’informazione l’entropia definisce la quantità minima delle componenti fondamentali (bit) necessarie a descriverla, esattamente come i gradi di libertà descrivono lo stato di un sistema fisico. In altre parole essa indica la misura del grado di complessità di una informazione: una singola nota, un suono monotonale, possiede pochissima informazione, mentre la IX Sinfonia di Beethoven ne contiene molta di più. Però attenzione: il suono ricavato da mille radioline sintonizzate ognuna su una diversa stazione è sostanzialmente inintelligibile ma nel suo complesso contiene molta più informazione di quanta ne abbia mai scritta il celebre compositore in tutta la sua vita. Per poter ascoltare la IX Sinfonia trasmessa da una sola radio dovremmo spegnere tutti gli altri ricevitori o alzare il volume di quella radiolina fino a sovrastare il rumore proveniente dalle altre, ossia compiere un lavoro o iniettare energia dall’esterno.

La termodinamica dei buchi neri


Le tre leggi della termodinamica dei buchi neri
Come per la termodinamica classica anche quella dei buchi neri ha le sue leggi non meno importanti. L’analogia tra i due insiemi di assiomi indica anche la strada da seguire per comprendere il bizzarro fenomeno.
Legge zero della  termodinamica dei buchi neri
Per  un buco nero stazionario la gravità all’orizzonte degli eventi è costante.
Questo sembra un concetto banale ma non lo è. Per qualsiasi corpo in rotazione su un asse anche se di forma perfettamente sferica la gravità non è costante alla sua superficie: ce ne sarà un po’ di più ai poli e un po’ meno al suo equatore. Questo principio ricorda che l’orizzonte degli eventi invece è un limite matematico dettato esclusivamente dall’equilibrio tra la gravità e la velocità della luce.
Prima legge della  termodinamica dei buchi neri
Nei buchi neri stazionari ogni variazione o apporto di energia comporta una modifica della sua area: $$d M={\frac{\kappa}{8\pi}}\,d A_{OE}\,+\,\Omega d J\,+\,\Phi d Q\,$$
I buchi neri sono descritti da solo tre parametri: la massa \(M\) , la carica elettrica \(Q\) e momento angolare \(J\) . Come nell’esempio nell’articolo è quindi possibile calcolare quanto varia l’area di un buco nero in cui una quantità di materia/energia diversa da zero cade oltre l’orizzonte degli eventi.
Tralasciando le note costanti naturali \(G\) e \(c\), \(\kappa\) indica la gravità superficiale all’orizzonte degli eventi, \(A_{OE}\) l’area di questo, mentre \(\Omega\) la velocità angolare, \(J\) il momento angolare, \(\Phi\) il potenziale elettrostatico, \(Q\) la carica elettrica sono propri del buco nero all’orizzonte degli eventi.
Questo complesso schema matematico è molto simile alla descrizione del Primo Principio Termodinamico dove si scopre che il differenziale energetico \(E\) è correlato alla temperatura \(T\), all’entropia \(S\) e alla capacità di svolgere un lavoro \(W\) in un sistema chiuso: $$dE=TdS\,+\,dW$$
Seconda legge della  termodinamica dei buchi neri
La somma dell’entropia ordinaria esterna al buco nero con l’entropia totale di un buco nero aumenta nel tempo come conseguenza delle trasformazioni generiche di questo: $$\Delta S_{o}\,+\,\Delta S_{BN}\,\geq\,0$$
Il Secondo Principio Termodinamico richiede che l’entropia di un sistema chiuso debba sempre aumentare come conseguenza di trasformazioni generiche. Se un sistema ordinario cade in un buco nero, la sua’entropia \(S_{o}\) diventa invisibile ad un osservatore esterno ma con questa interpretazione si esige che l’aumento dell’entropia del buco nero \(S_{BN}\) compensi la scomparsa di entropia ordinaria dal resto dell’universo. Con la scoperta della radiazione di Hawking è anche evidente il decremento della massa di un buco nero che essa comporta. Di conseguenza ci si dovrebbe aspettare che anche l’entropia connessa alla sua area diminuisca. Con questa interpretazione (Bekenstein, 1973) si tiene conto anche del fenomeno di evaporazione.
Terza legge della  termodinamica dei buchi neri
È impossibile annullare la gravità dell’orizzonte degli eventi con qualsiasi processo fisico.
Il Terzo Principio Termodinamico afferma che è fisicamente impossibile raggiungere una temperatura nulla tramite qualsiasi processo fisico.
Applicato ai buchi neri questa legge mostra come sia impossibile raggiungere una gravità nulla all’orizzonte degli eventi di un buco nero. In linea di principio aumentando la carica elettrica di un buco nero, sarebbe possibile cancellare l’orizzonte degli eventi e mostrare così finalmente la singolarità nuda. Tuttavia, l’energia che dovremmo iniettare nel buco nero sotto forma di particelle cariche sarebbe sempre più grande tanto più ci si avvicinasse al risultato senza mai poterlo raggiungere.

Un buco nero è causato dal collasso della materia o, per l’equivalenza tra materia ed energia, dalla radiazione, entrambi i quali possiedono un certo grado di entropia. Tuttavia, l’interno del buco nero e il suo contenuto non sono visibili ad un osservatore esterno. Questo significa che non è possibile misurare l’entropia dell’interno del buco nero.
Nell’articolo precedente [cite]https://ilpoliedrico.com/2017/03/il-principio-olografico-dei-buchi-neri-lorizzonte-degli-eventi.html[/cite] ho detto che un buco nero stazionario è parametrizzato unicamente dalla sua massa, carica elettrica e momento angolare. Secondo il No Hair Theorem tutto ciò che scompare oltre l’orizzonte degli eventi viene totalmente sottratto all’universo. Quello che potremmo percepire di un buco nero sono la sua massa, carica elettrica e momento angolare; pertanto le medesime proprietà possedute da un oggetto inghiottito da un buco nero verrebbero a sommarsi con le precedenti, contribuendo così alla loro espressione complessiva. In soldoni — trascurando per un attimo la sua carica elettrica e il momento angolare — un oggetto di massa \(m\) andrebbe a sommarsi a \(M_{BN}\) del buco nero, cosi che \(M_{BN}’\) finirebbe per essere \(m+M_{BN}\) facendo crescere anche la dimensione dell’orizzonte degli eventi.
Ma secondo questa interpretazione, null’altro rimarrebbe dell’oggetto finito oltre l’orizzonte degli eventi, la sua entropia andrebbe perduta per sempre. Questa interpretazione — come fece notare per primo Bekenstein — cozza però col Secondo Principio della Termodinamica che afferma che il grado di disordine – entropia – di un sistema chiuso — l’Universo è un sistema chiuso — può solo aumentare. Quindi qualsiasi cosa, materia o energia, che finisse oltre l’orizzonte degli eventi di un buco nero finirebbe per sottrarre entropia all’universo, e questo è inaccettabile.
L’unico modo per non contraddire questa legge fondamentale 2 è assumere che anche i buchi neri abbiano un’entropia.
Questa come si è visto dipende dalla massa/energia che cade in un buco nero e che va a sommarsi alla precedente, e, visto che per l’interpretazione classica niente può uscire da un buco nero, non può che aumentare col tempo. Ma anche le altre due proprietà, carica elettrica e momento angolare, contribuiscono nella loro misura a descrivere compiutamente un buco nero. Per ogni combinazione di questi tre parametri si possono perciò teorizzare altrettanti stati diversi riguardo ad esso; quello che ne esce è un concetto molto simile all’entropia legata ai possibili microstati della termodinamica statistica. L’entropia, ossia l’informazione di questi microstati, è pertanto distribuita sull’unica parte accessibile all’universo, la superficie dell’area dell’orizzonte degli eventi.
In natura la più piccola unità dimensionale di superficie è l’Area di Planck, quindi è naturale esprimere l’entropia di un buco nero in questa scala. Per descrivere matematicamente l’entropia \(S\) 3  di un buco nero di Schwarzschild partendo dall’area dell’orizzonte degli eventi \(A_{O E}\), allora dovremmo scrivere $$\tag{1}S_{buco nero}={A_{O E}\over 4 L_{P}^2}={c^3 A_{O E}\over 4 G \hbar}$$ dove \(L_{P}\) è la lunghezza di Plank, \(G\) è la Costante di Gravitazione Universale, \(\hbar\) la costante di Plank ridotta e \(c\) ovviamente la velocità della luce, sapendo che la suddetta area è condizionata unicamente dalla massa del buco nero $$\tag{2}A_{O E}=16\pi \frac{G^2M_{BN}^2}{c^4}$$.
Facciamo ad esempio l’ipotesi, che poi servirà in futuro per illustrare il Principio Olografico e che si rifà anche direttamente alla Prima Legge della Termodinamica dei Buchi Neri (vedi box qui accanto), di un fotone avente una lunghezza d’onda \(\lambda\) — la lunghezza d’onda di un fotone è inversamente proporzionale alla sua energia — che cade in un buco nero di massa \(M_{BN}\) e di conseguenza di raggio \(r_{S}\) da una direzione indeterminata.
Avvicinandosi all’orizzonte degli eventi suddetto fotone finirà per decadere fino ad avere una lunghezza d’onda paragonabile alla dimensione del raggio di Schwartzschild: \(\lambda\sim\pi r_{S}\).
L’energia rilasciata dal fotone nel buco nero quindi è $$\tag{3}d E = \frac{hc}{\lambda} = \frac{2\pi \hbar c}{r_{S}}$$
Per l’equivalenza tra massa ed energia — la stranota \(e=mc^2\) della Relatività Generale — la massa del buco nero finisce per crescere$$\tag{4}d M_{BN}=\frac{d E}{c^2} = \frac{2\pi \hbar}{c r_{S}}$$
Di conseguenza un aumento della massa, per quanto piccola, del buco nero finisce per far aumentare anche le dimensioni dello stesso nella misura $$\tag{5}d r_{S}=\frac{2G}{c^2} d M_{BN}=\frac{4\pi\hbar G}{c^3 r_{S}}$$
e anche l’area: $$\tag{6}d A_{OE}=4\pi d r_{S}^2 = 8\pi r_{S}d r_{S}=32\pi^2\frac{\hbar G}{c^3}$$

Anche se questo genere molto semplificato di buchi neri è solo teorico, permette però di esplorare la complessità del problema e di farsi un’idea delle dimensioni dell’entropia di un buco nero 4.